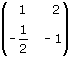Figura successiva
Figura precedente
Home

Autovettori e autovalori
è un autovettore per t se si ha t(v)=kv per un certo numero reale k (cioè se il trasformato di v è un multiplo di v); k prende il nome di autovalore per t relativo all'autovettore v.
Considera la trasformazione lineare di matrice
Si tratta di uno stiramento rispetto agli assi coordinati. Agendo sulla figura (facendo fare al vettore azzurro un giro completo attorno all'origine), verifica che:
Tutti i vettori con la punta sull'asse delle x (escluso il vettore nullo, s'intende e non lo diremo più), ad esempio v=[1, 0], sono autovettori, il relativo autovalore è 2. Ciò significa che l'asse delle x è retta unita cioè ogni suo punto è trasformato in un punto che appartiene ancora all'asse delle x.
Tutti i vettori con la punta sull'asse delle y, ad esempio v=[0, 1], sono autovettori, il relativo autovalore è 3. Anche l'asse delle y è retta unita per la trasformazione.
Non ci sono altri autovettori.
Considera la trasformazione lineare di matrice
Si tratta di un'omotetia con centro nell'origine e rapporto 2 (puoi pensare ad uno stiramento uniforme rispetto ad ogni direzione del piano). Agendo sulla figura, verifica che:
Tutti i vettori v = [x, y] del piano sono autovettori, il loro autovalore è 2. Ogni retta per l'origine è retta unita.
Considera la trasformazione lineare di matrice
Si tratta di una rotazione di 90° con centro nell'origine. Agendo sulla figura, verifica che:
Non esistono autovettori. Ogni vettore v viene trasformato in un vettore v' ruotato di 90° e di stesso modulo (ovviamente, perchè si tratta di un'isometria).
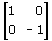
Considera la trasformazione lineare di matrice
Si tratta di una simmetria rispetto all'asse delle x. Agendo sulla figura, verifica che:
I vettori che hanno la punta sull'asse delle x oppure sull'asse delle y sono autovettori (di autovalore 1, perchè si tratta si un'isometria).
L'asse delle y è asse unito ma nessun suo punto, a parte l'origine, è unito. L'asse delle x è asse unito e, di più, ogni suo punto è punto unito.
Considera la trasformazione lineare di matrice
Si tratta di una simmetria rispetto all'origine. Agendo sulla figura, verifica che:
Tutti i vettori v = [x, y] del piano sono autovettori, il loro autovalore è 1 (perchè si tratta di un'isometria). Ogni retta per l'origine è retta unita.
Sia t la trasformazione lineare di matrice
Un vettore non nullo
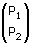
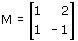
Nella figura dinamica seguente puoi impostare i valori a, b, c, d della matrice M (trascinandoli sull'asse delle x); in tal modo resta definita la trasformazione lineare t(v)=Mv. Puoi inoltre trascinare il vettore azzurro che rappresenta un generico vettore v del piano (devi afferrare il vettore per la punta). Il vettore rosso è il trasformato di v (ed è quindi dipendente, non trascinabile, varia al variare di v). Per determinare gli eventuali autovettori di t devi vedere se, trascinando il vettore azzurro, puoi allinearlo col vettore rosso. Trovato un allineamento, cioè un autovettore, leggi il corrispondente autovalore k nel campo grigio. Ad esempio ogni vettore del piano è autovettore per la trasformazione identica con relativo autovalore 1 (prova!). Per traslare l'intero piano, trascinalo tenendo premuto il pulsante destro del mouse; per cambiare la scala trascina una graduazione.

Esperimento 1
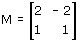

Esperimento 2

Esperimento 3
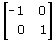

Esperimento 4
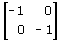

Esperimento 5