Indice    Paragrafo precedente    Paragrafo successivo

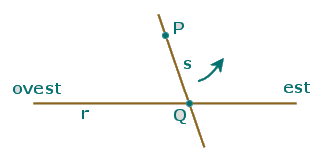Nella figura qui a fianco la retta r è fissa mentre la retta s può ruotare in senso antiorario attorno al punto P. Indichiamo con Q il punto in cui r ed s si incontrano.


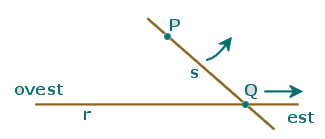Man mano che s ruota si vede che il punto Q si allontana verso est sulla retta r.


Il punto Q si muove con continuità su r: piccole rotazioni di s determinano piccoli spostamenti di Q (e viceversa). Q assume via via tutte le posizioni possibili su r, "passa" per tutti i punti di r.

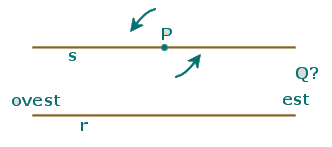Il punto Q dunque si allontana sempre più sulla retta r. Si intuisce però che esiste una (e una sola) situazione in cui sembra proprio che le due rette non si intersechino e quindi Q non esista. In questa situazione le due rette si dicono parallele.


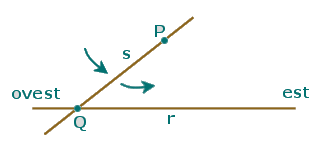Continuando a ruotare s ci accorgiamo che il punto Q ricompare su r, questa volta però Q è a ovest. Eccoci arrivati a un punto cruciale. Nella geometria euclidea si assume, assecondando l'intuizione, che per un punto P non appartenente alla retta r passi una e una sola retta s parallela a r (tale cioè che r e s non si incontrino). Tale assunzione non è altro che il quinto postulato di Euclide.

Quinto postulato


Qui di seguito sono elencati i postulati su cui Euclide (300 avanti Cristo) fondò, negli Elementi, il castello della sua geometria:

• (P1) Da ogni punto a ogni altro punto è possibile condurre una linea retta.
  
  Euclide non postula esplicitamente che per due punti passi un'unica retta, ma assume tacitamente che sia così.
  
  

• (P2) Un segmento di linea retta può essere indefinitamente prolungato in linea retta.
  
  

• (P3) Attorno ad un centro scelto a piacere è possibile tracciare una circonferenza con raggio scelto a piacere.
  
  

• (P4) Tutti gli angoli retti sono uguali.
  
  Euclide ha già dato la definizione di angolo retto: se una retta r innalzata da un'altra retta s forma con essa angoli adiacenti uguali fra loro, ciascuno dei due angoli è retto. Il postulato P4 è necessario per garantire che gli angoli ottenuti con un'altra costruzione di questo tipo, relativa alle rette r' e s', sono uguali ai precedenti. Il postulato P4 dimostra una notevole raffinatezza logica da parte di Euclide e afferma in sostanza che il piano è uniforme (nel senso che la costruzione predetta fornisce sempre gli stessi angoli, in qualsiasi parte del piano venga eseguita).
  
  

• (P5) In un piano, per un punto fuori di una retta data si può condurre una e una sola parallela a tale retta (due rette si diranno, con Euclide, parallele, quando non si incontrano).
  
  In realtà Euclide formulò il quinto postulato in una forma diversa da quella qui riportata ma ad essa del tutto equivalente.