Indice    Paragrafo precedente    Paragrafo successivo   

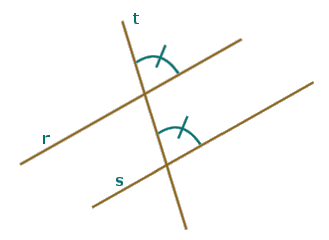Consideriamo due rette parallele r ed s e una terza retta t che le tagli. Si intuisce che gli angoli evidenziati in figura qui a fianco, chiamati angoli corrispondenti, devono essere uguali (o meglio congruenti cioè sovrapponibili): la retta t ha infatti la stessa inclinazione rispetto alle rette r ed s che sono parallele. Potete immaginare di muovere rigidamente un angolo fino a sovrapporlo all'altro, facendo "scorrere" la retta t su se stessa (si tratta di una traslazione).

Rette parallele tagliate da una trasversale (angoli corrispondenti)

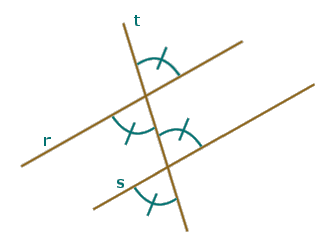
Da questa osservazione e dall'uguaglianza di angoli opposti al vertice segue l'uguaglianza dei quattro angoli acuti che si formano (vedi figura seguente).

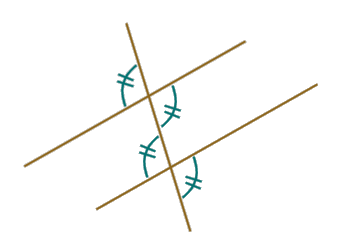
Analogamente si intuisce che i quattro angoli ottusi della figura seguente sono tutti tra loro uguali.

Si dimostra il seguente teorema:

Teorema 1 Se due rette r ed s sono parallele e t è una trasversale allora vengono a formarsi quattro angoli acuti uguali e quattro angoli ottusi uguali (oppure si formano otto angoli retti).

Ora attenzione: questa proprietà delle rette parallele, che come si è visto ha una sua evidenza intuitiva, può essere dimostrata, sul piano logico, solo se si assume il quinto postulato di Euclide. Pur non volendo ripercorrere tutti i passaggi logici necessari a dimostrare questa fondamentale proprietà, cerchiamo di capire perché tale dimostrazione richiede il quinto postulato (*). A questo proposito utilizzeremo il teorema inverso del precedente che può dimostrarsi senza far uso del quinto postulato e che riportiamo qui per comodità

Teorema 2 Se due rette r ed s formano con una trasversale t angoli corrispondenti uguali allora le rette r ed s sono parallele.

Allora il teorema che vogliamo dimostrare ha per ipotesi

le rette r ed s sono parallele e t è una trasversale

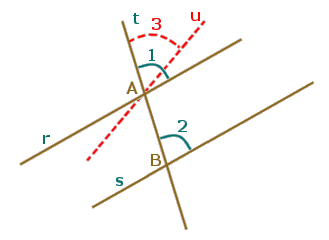
gli angoli corrispondenti 1 e 2 indicati in figura qui a fianco sono uguali (congruenti)

Euclide procede "per assurdo". Supponiamo per assurdo che gli angoli 1 e 2 non siano uguali; potremo allora tracciare una retta u, passante per il punto A, che formi con t un angolo 3 uguale all'angolo 2. Tale retta è distinta da r, a causa del diverso angolo che forma con t, ed è parallela ad s in forza del teorema 2. Ciò contraddice il quinto postulato: per il punto A passerebbero due distinte rette parallele ad s (le rette r ed u). Allora gli angoli 1 e 2 devono essere uguali. Notate che qui la questione cruciale è l'unicità della parallela per A.