Indice Paragrafo precedente Paragrafo successivo

9. Il concetto unificante di linea geodetica
Consideriamo una qualsiasi superficie (la superficie di un cilindro, di una sfera, di un cono, di un toro o anche un piano). Indichiamo con la lettera Σ tale superficie. Come potremmo definire su Σ delle linee che equivalgano alle linee rette del piano euclideo? Ecco la definizione che ci serve:
Definizione Diremo che una linea γ tracciata sulla superficie Σ è una linea geodetica se ogni arco non troppo lungo di γ, i cui estremi siano i punti A e B, è il percorso più breve da A a B tra tutti quelli tracciabili su Σ.
Ci si rende subito conto che le linee geodetiche del piano euclideo sono le rette; ci si rende anche conto, sulla base di quanto detto nei paragrafi precedenti, che le circonferenze massime sono le geodetiche sulla superficie di una sfera tenendo presente che, sulla sfera, archi non troppo lunghi di circonferenze massime sono necessariamente archi minori.
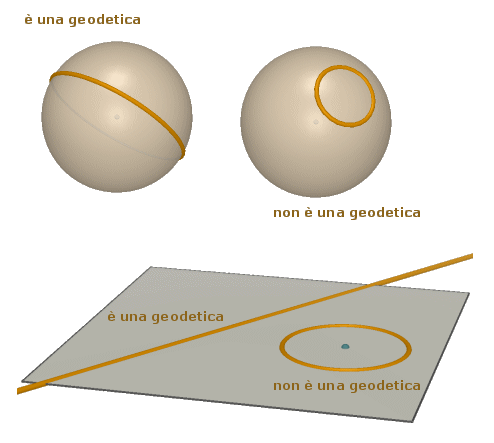
Osservate la figura seguente. Sulla prima sfera è stata tracciata una geodetica (una circonferenza massima), sulla seconda una linea che non è una geodetica (una circonferenza minore, cioè una circonferenza ottenuta come sezione mediante un piano che non passa per il centro della sfera); tra poco ci renderemo conto che comunque presi due punti A e B su una circonferenza minore, l'arco (minore) AB non rappresenta mai il percorso minimo tra A e B. Vedete poi la situazione analoga nel piano euclideo: una retta, quindi una geodetica, e una circonferenza (qualsiasi) che non è mai una geodetica.
La nozione di linea geodetica è piuttosto astratta ma proprio per questo unificante: enti geometrici che siamo abituati a pensare come sostanzialmente diversi (ad esempio rette euclidee di E2 e circonferenze massime di S2) diventano casi particolari di un concetto generale di "linea più breve". Ed è proprio l'idea intuitiva di "linea più breve" o di "linea più dritta" che aiuta ad avvicinarci a questo nuovo concetto.
Naturalmente il nostro approccio alla nozione di linea geodetica è informale e intuitivo; in particolare si noterà la mancanza di rigore nella locuzione "non troppo lungo" riferita ad un arco di curva (ma nei prossimi paragrafi illustreremo la necessità di questa condizione). Il settore della matematica che si occupa della geometria delle superfici curve (e quindi dello studio delle linee geodetiche) è la geometria differenziale ed è uno dei rami più tecnici e più difficili della matematica moderna. I primi ad occuparsi di geometria differenziale sono stati i grandi matematici tedeschi Gauss e Riemann (allievo di Gauss, vedi cronoasse). Il primo trattato di geometria differenziale (Disquisitiones circa superficies curvas), di Gauss, è del 1827.