Indice Paragrafo precedente Paragrafo successivo

11. Geodetiche sul cubo
E' chiaro che su ogni faccia di un cubo gli archi geodetici sono segmenti; l'unica cosa da capire è come una linea geodetica "attraversi" uno spigolo. Osservate la scatola in figura (non è essenziale che sia cubica): un elastico è stato teso tra i punti P e Q che si trovano su facce consecutive.
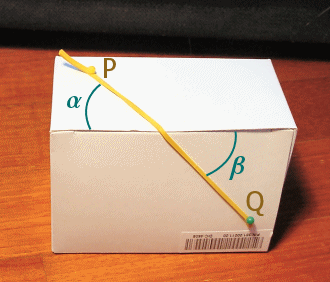
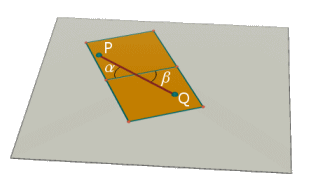 Ci rendiamo conto di una semplice regola che caratterizza le geodetiche sul cubo: gli angoli α e β che l'elastico forma con lo spigolo sono uguali. Del resto se rappresentassimo le due facce in questione nel piano (vedi figura a fianco) ci renderemmo conto che gli angoli α e β sono angoli opposti al vertice.
Ci rendiamo conto di una semplice regola che caratterizza le geodetiche sul cubo: gli angoli α e β che l'elastico forma con lo spigolo sono uguali. Del resto se rappresentassimo le due facce in questione nel piano (vedi figura a fianco) ci renderemmo conto che gli angoli α e β sono angoli opposti al vertice.
Nella figura seguente vedete due linee geodetiche r ed s. Per un essere bidimensionale che si muovesse sul cubo sarebbero percorsi intrinsecamente "rettilinei". L'attraversamento degli spigoli rispetta infatti la regola che abbiamo enunciato. Un essere bidimensionale non potrebbe rendersi conto in alcun modo dell'attraversamento di uno spigolo. I punti di uno spigolo sono dal suo punto di vista perfettamente equivalenti a quelli che per noi si trovano, ad esempio, nella parte centrale di una faccia. Noi percepiamo uno spigolo in quanto intersezione di due facce disposte, nello spazio tridimensionale, su piani diversi.
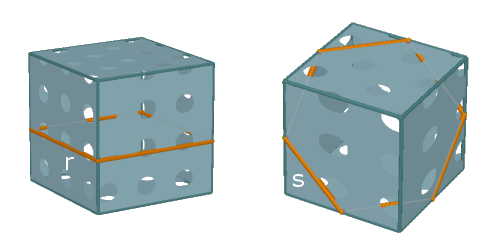
Possiamo convincerci che le linee r ed s sono geodetiche anche considerando due opportuni sviluppi del cubo nel piano (vedi figura seguente): le linee r ed s sulla superficie del cubo corrispondono a due segmenti sullo sviluppo (i cui estremi saranno identificati quando il cubo verrà assemblato nello spazio).
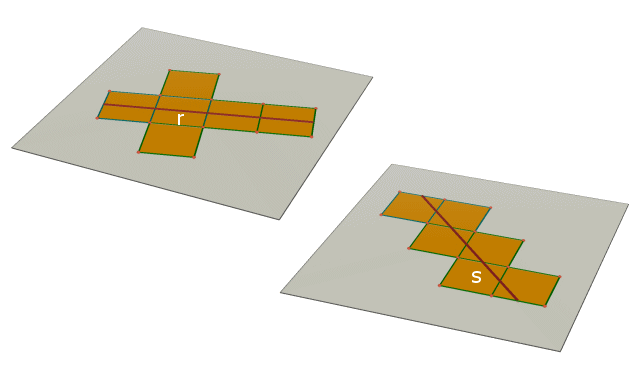
Le due geodetiche r e s appaiono, dal nostro punto di vista tridimensionale, rispettivamente come un quadrato e come un esagono regolare (possiamo ottenerle segando la superficie del cubo con due piani opportuni); ma dal punto di vista intrinseco di una creatura bidimensionale sarebbero delle rette.
 Sezioni del cubo con piani perpendicolari a una diagonale
Sezioni del cubo con piani perpendicolari a una diagonale
 Sezioni del cubo (animazione)
Sezioni del cubo (animazione)
 Domanda
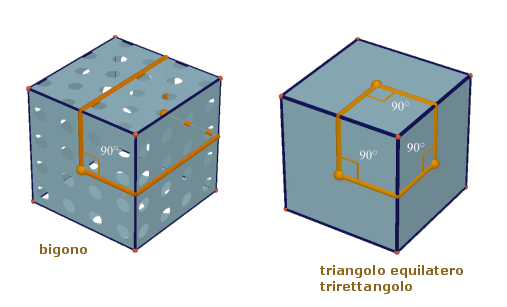
Nel piano euclideo non esistono poligoni con meno di tre lati; ciò può invece accadere se il nostro ambiente geometrico bidimensionale è la superficie di un cubo (o di una sfera). Sapete tracciare sul cubo un bigono, cioè un poligono con due lati? Provate anche a tracciare un triangolo equilatero con tre angoli retti. (E' chiaro che i lati di un poligono devono tutti essere archi geodetici).
Domanda
Nel piano euclideo non esistono poligoni con meno di tre lati; ciò può invece accadere se il nostro ambiente geometrico bidimensionale è la superficie di un cubo (o di una sfera). Sapete tracciare sul cubo un bigono, cioè un poligono con due lati? Provate anche a tracciare un triangolo equilatero con tre angoli retti. (E' chiaro che i lati di un poligono devono tutti essere archi geodetici).
[Soluzione. La figura seguente mostra i due poligoni; osservate che il bigono ha due angoli retti.]