Indice    Paragrafo precedente    Paragrafo successivo   

Il nostro scopo è ora quello di determinare una formula che ci fornisca la somma degli angoli di un triangolo sferico. A questo fine dovremo misurare gli angoli in radianti (anziché in gradi) e calcolare l'area di fusi sferici. Risolviamo rapidamente le due questioni.



Misura degli angoli in radianti

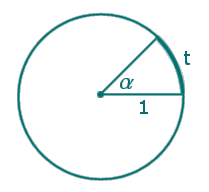Consideriamo la circonferenza di raggio unitario della figura a fianco. Ad ogni angolo al centro α corrisponde un arco di circonferenza t e viceversa. Tra angoli e archi c'è una relazione di proporzionalità diretta: se si raddoppia l'angolo si raddoppia anche l'arco, se si triplica l'angolo si triplica anche l'arco, ecc. (e viceversa). Possiamo quindi assumere come misura dell'angolo la misura dell'arco corrispondente. Parleremo in questo caso di misura dell'angolo in radianti. Ad esempio ad un angolo di 90° corrisponde un arco di lunghezza π/2; quindi la misura in radianti di un angolo di 90° è π/2. In generale possiamo scrivere la proporzione

α : 360 = t : 2π

dove α è la misura in gradi dell'angolo e t la lunghezza dell'arco corrispondente (quindi t è la misura in radianti dell'angolo). Ne segue

t = πα/180

Quest'ultima formula ci consente di passare dalla misura in gradi di un angolo a quella in radianti. Viceversa possiamo passare dalla misura in radianti a quella in gradi con la formula

α = 180t/π

Area di un fuso sferico

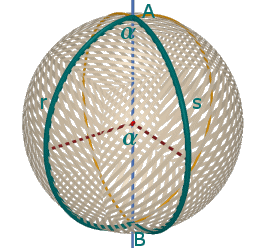Un fuso sferico è la regione della superficie sferica compresa tra due semicirconferenze massime (ed è la parte che non contiene i prolungamenti delle semicirconferenze). Nella figura a fianco è evidenziato in verde un fuso sferico: r ed s sono due circonferenze massime e AB è un diametro della sfera. E' anche evidenziato l'angolo α del fuso. Si capisce che l'area di un fuso è direttamente proporzionale all'angolo del fuso (che può variare tra 0° e 180°); si può quindi scrivere la proporzione

α : π = A : 2π

dove α è l'angolo del fuso espresso in radianti, π è l'angolo piatto espresso in radianti, A è l'area del fuso e 2π è l'area della superficie della semisfera (ricordando che il raggio della sfera è 1). Ne segue

A = 2α

ove α è l'angolo del fuso espresso in radianti. Ad esempio un fuso di angolo π/2 ha area π, costituendo infatti 1/4 della superficie sferica.

Fusi sferici

Fusi sferici con prolungamenti

E' infine evidente che l'area del doppio fuso sferico della figura seguente è

A = 4α