Esperimenti

Indice Avanti Indietro

10. Esperimenti
         Istruzioni esaminate: wait

Operare in ambiente Logo significa, spesso, fare della sperimentazione geometrica. Ce ne renderemo conto in questo numero in cui lo studio di una procedura semplicissima ci condurrà a risultati sorprendenti e ci mostrerà collegamenti inaspettati con l'aritmetica. Un consiglio: fate anche dei vostri esperimenti, provate ad apportare delle modifiche alle procedure che troverete.

Il punto di partenza è lo studio dei poligoni regolari. Noi conosciamo già un procedura per tracciarli. Come ricorderete, la procedura è questa
to PoligonoRegolare :N :LATO
   repeat :N [fd :LATO rt 360/:N]
end

Qui si parte dal numero N dei lati e si costruisce il poligono ricavando l'ampiezza della rotazione da ripetere in funzione di N.

Ma si può assumere un altro punto di vista. Facciamo avanzare la tartaruga di un certo numero di passi, facciamola ruotare di un certo angolo, facciamole ripetere continuamente questa stessa sequenza. E stiamo a vedere cosa succede. Non sappiamo, a priori, quanti saranno i vertici della figura che sarà generata. Ecco una prima versione ricorsiva di questa procedura
to NuovoPoligono :LATO :ANGOLO
   fd :LATO
   rt :ANGOLO
   NuovoPoligono :LATO :ANGOLO
end

Come vedete si tratta di una procedura molto semplice, probabilmente la più semplice che possiamo considerare in ambiente Logo. Mettiamola in esecuzione chiamando, ad esempio,
NuovoPoligono 100 90

Viene tracciato, in questo caso, un quadrato di lato 100. E' chiaro, gli angoli sono di 90°, la figura si chiude dopo quattro rotazioni. Osservate però che la tartaruga non si ferma, continua a ripercorrere la figura all'infinito. Non ce ne meravigliamo, visto che per il momento non abbiamo introdotto nella procedura (ricorsiva!) una condizione d'arresto (un'istruzione stop). Per interrompere l'esecuzione useremo il pulsante "halt" della finestra commander. Digitando
NuovoPoligono 100 120

otterremo invece un triangolo equilatero, qui la figura si chiude dopo tre rotazioni. E se l'angolo in input fosse di 72 gradi otterremmo un pentagono regolare. E' chiaro quindi che la procedura NuovoPoligono è in grado di generare tutti i poligoni regolari che ben conosciamo: per ottenerne uno con n lati, l'angolo in input dovrà essere 360/n.

Questa volta però abbiamo altre possibilità, possiamo considerare angoli non ottenibili con la formula 360/n (n numero intero). Abbiamo appena visto che se l'angolo è di 90 gradi otteniamo un quadrato, mentre se è di 72 gradi otteniamo un pentagono regolare. Cosa succederà se prenderemo un valore intermedio tra questi due valori, ad esempio un angolo di 80 gradi? La struttura della procedura (avanzamenti tutti uguali, rotazioni tutte uguali) ci spinge a ritenere che la figura generata debba essere un poligono regolare. Ma noi sappiamo che non esistono poligoni regolari tra il quadrato e il pentagono. E allora? Non ci rimane che provare.

La schermata seguente mostra l'effetto della procedura NuovoPoligono 100 80.

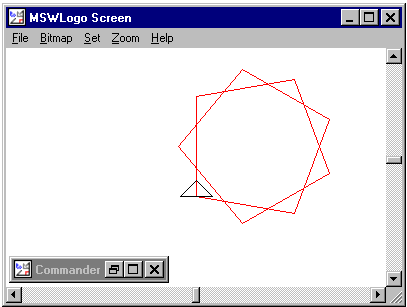
Che figura abbiamo ottenuto? A prima vista sembrerebbero due pentagoni sovrapposti, ma non è così. Si tratta di un unico poligono intrecciato con 9 lati (e quindi 9 vertici). Ed è un poligono intrecciato regolare perché i lati sono tutti uguali e gli angoli sono tutti uguali. E' una scoperta interessante visto che di solito si considerano solo poligoni non intrecciati. Ci chiediamo, qual è somma di tutte le rotazioni eseguite dalla tartaruga per chiudere la figura? Poiché la figura mostra 9 vertici, ci sono state 9 rotazioni della tartaruga ciascuna di 80 gradi. Quindi la rotazione totale accumulata per chiudere la figura è in questo caso di 9·80=720 gradi. E' cioè esattamente di due giri. Cominciamo a capire: se la rotazione totale è di 360 gradi la procedura genera un ordinario poligono regolare, se è maggiore di 360 gradi il poligono è intrecciato. Inoltre ci siamo resi conto che la rotazione totale è un multiplo di 360° (720°=360°·2). E' allora abbastanza naturale formulare questa congettura: qualsiasi poligono generato con la nostra procedura si chiude non appena la rotazione totale raggiunge un multiplo di 360. Per verificare questa ipotesi operiamo qualche modifica alla nostra procedura (per eseguire la procedura non ridigitate il codice ma copiatelo e incollatelo direttamente nell'editor di MSWLogo)
to NuovoPoligono :LATO :ANGOLO
   cs
   make "SommaRotazioni 0
   esegui :LATO :ANGOLO
end

to esegui :LATO :ANGOLO
   fd :LATO
   wait 60
   rt :ANGOLO
   wait 60
   make "SommaRotazioni :SommaRotazioni + :ANGOLO
   if (remainder :SommaRotazioni 360) = 0 ~
      [print :SommaRotazioni stop]
   esegui :LATO :ANGOLO
end

Come vedete in questa nuova versione della procedura NuovoPoligono teniamo il conto delle rotazioni via via eseguite. La variabile SommaRotazioni che all'inizio vale 0 viene incrementata dopo ogni rotazione di un valore pari a quest'ultima (istruzione make). Inoltre abbiamo introdotto una condizione di arresto per la procedura ricorsiva esegui (istruzione if): se SommaRotazioni, cioè la rotazione totale, è un multiplo di 360 allora visualizziamo il valore di SommaRotazioni e interrompiamo la procedura. Infine l'istruzione wait 60, che viene eseguita dopo ogni avanzamento e dopo ogni rotazione, serve a rallentare l'esecuzione della procedura e ci consente di poter osservare tranquillamente i vari passi di costruzione della figura (in effetti wait 60, ogni volta che viene chiamata, ferma l'esecuzione per 60 sessantesimi di secondo). Il carattere ~ (tilde) che trovate nel codice indica che il comando continua alla riga seguente. Bene, possiamo ora fare qualche esperimento. Osservate la schermata seguente, ottenuta chiamando NuovoPoligono 100 108.

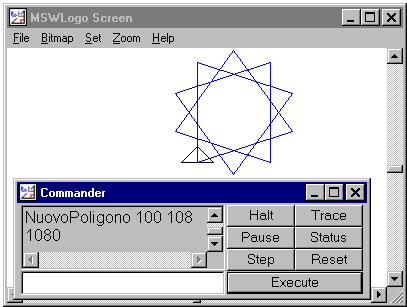
Come vedete questa volta, non appena chiusa la figura, la tartaruga si arresta. Il numero, 1080, che leggete nella finestra commander è la rotazione totale. Poiché ogni rotazione eseguita è di 108°, il numero di rotazioni eseguite (e quindi anche il numero di vertici e di lati) è 1080/108=10. Abbiamo dunque la conferma che la figura si chiude non appena la rotazione totale raggiunge un multiplo di 360 (in effetti 1080 è proprio il minimo comune multiplo di 108 e 360). La schermata seguente è stata ottenuta chiamando NuovoPoligono 140 160.

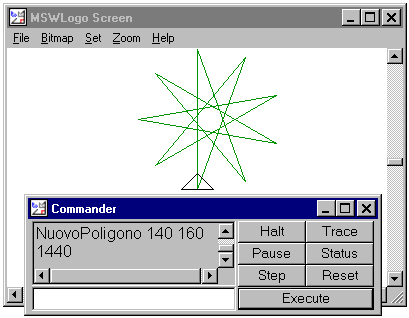
Anche in questo caso la nostra ipotesi trova conferma: la figura si chiude non appena la rotazione totale, che è necessariamente un multiplo di 160, diventa anche multiplo di 360. E quindi, di nuovo, ci rendiamo conto che la rotazione totale pari a 1440 è il mcm di 160 e 360. Vediamo inoltre che il numero dei vertici è 9 (=1440/160) e ciò dovrebbe meravigliarci. Non avevamo già trovato un poligono intrecciato regolare con 9 vertici (9 lati)? Certo, la prima schermata ne mostra proprio uno in cui l'angolo esterno è di 80° (e quindi quello interno è di 100°). Mentre qui l'angolo esterno è di 160° (e quello interno di 20°). Si tratta allora di forme diverse. La procedura NuovoPoligono non finisce di sorprenderci: ci siamo resi conto che per un dato n esistono più forme di poligoni regolari intrecciati con n lati (ad esempio per n=9 ne abbiamo già trovate 2, ma ce ne saranno delle altre?). Non si tratta di una scoperta da poco, sappiamo infatti che nel caso dei poligoni regolari non intrecciati ad ogni valore di n è associata un'unica forma. Detto in altro modo: per un dato n gli n-agoni regolari non intrecciati sono tutti simili mentre ciò non è vero per quelli intrecciati.

La nostra ricerca sui poligoni intrecciati potrebbe finire qui. Ma con un piccolo sforzo da parte dei ragazzi possiamo cogliere un risultato importante. Cerchiamo di mettere in formula ciò che abbiamo scoperto. Consideriamo allora un qualsiasi poligono generato con la nostra procedura e indichiamo con n il numero dei suoi vertici (e quindi dei suoi angoli e dei suoi lati) e con α l'angolo di rotazione della tartaruga. Abbiamo capito che la figura si chiude non appena la rotazione totale raggiunge un multiplo di 360 e poiché, per ipotesi, la figura si chiude dopo n rotazioni si deve avere n·α=k·360, dove k è un numero intero e n è il più piccolo numero intero tale che n·α sia multiplo di 360. Stante questa condizione su n, è facile rendersi conto che n e k non possono avere un fattore primo in comune. Infatti se avessero un fattore primo in comune potremmo dividere entrambi i membri dell'equazione n·α=k·360 per tale fattore pervenendo all'equazione n'·α=k'·360 con n' minore di n e ciò è impossibile. Quindi n e k sono numeri primi tra loro. Allora sappiamo che α=(k/n)360 con k e n primi fra loro.

Applichiamo questo risultato a n=9. I numeri minori di 9 e primi con 9 sono 1, 2, 4, 5, 7, 8. Gli angoli α corrispondenti sono (1/9)·360=40, (2/9)·360=80, (4/9)·360=160, (5/9)·360=200, (7/9)·360=280, (8/9)·360=320. E questa è la situazione

per α uguale a 40° o 320° otteniamo l'ennagono regolare non intrecciato (nel primo caso percorso in senso orario dalla tartaruga, nel secondo in senso antiorario);

per α uguale a 80° o 280° otteniamo l'ennagono della prima schermata (in senso orario o antiorario);

per α uguale a 160 o 200° otteniamo l'ennagono della terza schermata (in senso orario o antiorario).

Quindi non esistono altri ennagoni regolari intrecciati oltre a quelli già visti.

Come ulteriore esempio studiamo la situazione per n=36. I numeri minori di 36 e primi con 36 sono 1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35. Gli angoli α corrispondenti sono 10°, 50°, 70°, 110°, 130°, 170°, 190°, 230°, 250°, 290°, 310°, 350°. Ci siamo resi conto che le figure si presentano a coppie identiche (una costruita in senso orario e l'altra in senso antiorario). La coppia di angoli 10° e 350° determina il poligono regolare non intrecciato di 36 lati. Le altre cinque coppie determinano i poligoni regolari intrecciati che vedete nella figura seguente. Possiamo allora concludere che esistono cinque forme diverse per i 36-agoni regolari intrecciati.