Attività successiva
Attività precedente
Indice
Home

Attività 1 - Le trasformazioni lineari del piano
La forma più conveniente per esprimere tale trasformazione è quella matriciale; ecco il foglio di lavoro di Derive
Nota che alla riga #3 il trasformato del punto P è ottenuto moltiplicando la matrice M (matrice quadrata 2x2) per il vettore [P sub 1, P sub 2] che va considerato come matrice colonna
Mostriamo che la condizione ad - bc
nelle incognite x e y ammette una e una sola soluzione comunque si scelga il punto [x', y']; procedendo con Derive
Come vedi alla riga #10, la soluzione esiste ed è unica se e solo se il denominatore ad - bc è diverso da zero o, equivalentemente, il determinante di M è diverso da 0; ricorda infatti che
Osservazione 1 Ti sei dunque reso conto che ogni trasformazione lineare del piano individua una matrice
al quadrato individuato dai vertici P1=[1, 1], P2=[1, 2], P3=[2, 2], P4=[2, 1]. Cosa osservi? (Procedi da solo prima di leggere quanto segue.)
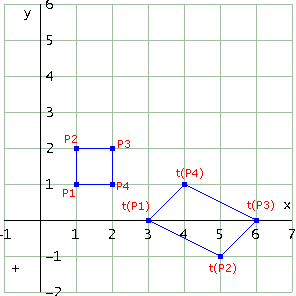
E questa è la rappresentazione grafica relativa alle righe #18 e #25 (il quadrato e il suo trasformato)
Per quanto concerne il codice di Derive, osserva che alla riga #24 abbiamo utilizzato il comando
per generare i vertici della figura trasformata. Puoi interpretare il comando così: genera il vettore dei punti t(P) al variare di P nel vettore quadrato (quadrato è un vettore di vettori, ti è chiaro?).
allo stesso quadrato dell'esperimento precedente. Cosa osservi?
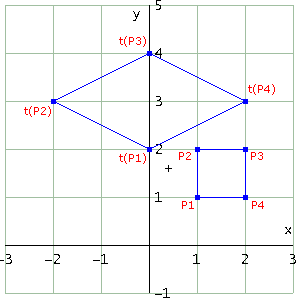
E questa è la rappresentazione grafica relativa alle righe #18 e #30
Notiamo che questa volta la trasformazione, la cui matrice ha determinante positivo, non ha mutato l'orientamento della figura: quadrato e parallelogramma (cioè il trasformato) hanno entrambi i vertici che si susseguono in senso orario. Si potrebbe dimostrare in generale che se una trasformazione lineare ha matrice con determinante positivo conserva l'orientamento mentre se ha matrice con determinante negativo lo inverte. E' facile calcolare anche stavolta l'area della figura trasformata: è 4. Si potrebbe dimostrare che, in generale, l'area della figura trasformata è uguale all'area della figura di partenza per il valore assoluto del determinante della matrice M che individua la trasformazione.
La matrice della simmetria rispetto all'asse delle y è
La matrice della simmetria rispetto all'origine è
Nota che i determinanti delle tre matrici sono tutti non nulli (quindi è verificata la condizione di biunivocità) e rispettivamente valgono -1, -1 ed 1 in accordo col fatto che le simmetrie non alterano l'area; inoltre le simmetrie rispetto agli assi invertono l'orientamento mentre la simmetria rispetto all'origine lo conserva.
Verifichiamo che una generica trasformazione lineare ha l'origine come punto unito
Una simmetria rispetto all'asse delle x lascia "fermi" tutti i punti dell'asse delle x, cioè tutti i punti del tipo [x, 0]. Verifichiamolo
Ecco quindi un esempio di trasformazione lineare che ha infiniti punti uniti. Una traslazione, se si esclude quella le cui componenti siano entrambe nulle, non ha invece punti uniti perchè, come sai, "muove" tutti i punti del piano. Quindi una traslazione (di vettore non nullo) non è mai una trasformazione lineare.
non sono riconducibili a quelle che definiscono una trasformazione lineare. E' solo una questione terminologica che deve però esserti ben chiara.
Osserva che sono verificate due condizioni necessarie affinchè esista una trasformazione lineare: l'origine è un punto fisso e si conserva il parallelismo. Se la trasformazione esiste ci aspettiamo inoltre che la sua matrice abbia determinante positivo, uguale a 4 (perchè?). Ecco il codice di Derive
Osserva che le quattro equazioni della riga #52 equivalgono in realtà ad otto equazioni algebriche ordinarie; ad esempio l'equazione
e applicala al quadrato dell'esperimento 5. La matrice, come vedi, ha determinante nullo. Cosa si può dire, sul piano geometrico, della corrispondenza?
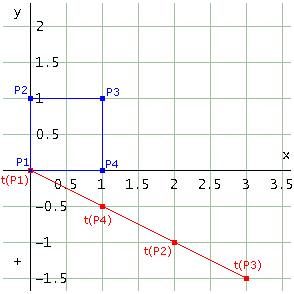
E questa è la rappresentazione grafica del quadrato e del suo trasformato
Questa volta la corrispondenza non è biunivoca: il quadrato degenera in un segmento. Ogni punto del piano viene trasformato in un punto della retta r individuata dai punti t(P1) e t(P2). Tutti i punti del piano "collassano" nella retta r. Se un punto appartiene ad r è immagine di infiniti punti del piano, se non appartiene ad r non è immagine di alcun punto del piano. Puoi verificarlo facilmente. Scegli un punto a piacere della retta r, ad esempio il punto Q = [3/2, -3/4], e determina tutti i punti del piano che hanno per immagine Q. Ecco il codice
Come vedi gli infiniti punti della forma [x, (3 - 2x)/4], cioè tutti i punti della retta y = (3 - 2x)/4, hanno per immagine Q. Prova ora tu a verificare che un punto non appartenenete ad r non è immagine di alcun punto del piano.
Cosa puoi dire della trasformazione?
Come vedi, ogni punto del piano viene trasformato in se stesso o, se vuoi, ogni punto del piano è punto unito. Si tratta della trasformazione che in realtà non trasforma nulla: prende il nome di trasformazione identica o identità. La matrice I si chiama matrice unità o matrice identica. Ti renderai conto nel seguito che la nozione di trasformazione identica è molto comoda.
Una trasformazione lineare del piano, chiamiamola t, è definita dalle equazioni
x' = ax + by
con ad - bc non nullo e trasforma il punto
y' = cx + dy
P = [x, y]
nel punto
t(P) = [x', y'] = [ax + by, cx + dy].

(matrice 2x1). Ricorda che l'operatore SUB di Derive serve ad estrarre le componenti di un vettore: P sub 1 è la prima componente di P, P sub 2 la seconda. La riga #5 si ottiene semplificando la #4.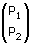
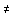 0 è necessaria e sufficiente affinchè la corrispondenza tra punti del piano sia biunivoca. Dire che la corrispondenza è biunivoca equivale infatti a dire che il sistema di due equazioni
0 è necessaria e sufficiente affinchè la corrispondenza tra punti del piano sia biunivoca. Dire che la corrispondenza è biunivoca equivale infatti a dire che il sistema di due equazioni
x' = ax + by
y' = cx + dy


con det(M)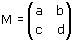
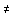 0. Viceversa ogni matrice di questo tipo individua una trasformazione lineare.
0. Viceversa ogni matrice di questo tipo individua una trasformazione lineare.

Esperimento 1
Applica la trasformazione lineare individuata dalla matrice
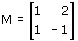

Ecco il codice di Derive

VECTOR(t(P), P, quadrato)
Sul piano geometrico osserviamo che la trasformazione porta punti distinti in punti distinti e infatti l'immagine del quadrato di partenza è un quadrilatero (ciò in accordo col fatto che det(M) è non nullo). Ma c'è di più: il quadrato si trasforma in un parallelogramma quindi si direbbe che si conservi il parallelismo (lati paralleli si trasformano in lati che sono ancora paralleli). In effetti è proprio così, come dimostreremo in seguito: una trasformazione lineare trasforma rette parallele in rette che sono ancora parallele. Inoltre notiamo che la trasformazione ha mutato l'orientamento della figura: nel quadrato i vertici si susseguono in senso orario mentre nella figura trasformata in senso antiorario (sarà sempre così?). Mutano inoltre lunghezze di lati corrispondenti e misure di angoli corrispondenti. E' facile calcolare, per sottrazione, l'area della figura trasformata: è 3. Mentre l'area del quadrato di partenza è 1. Puoi congetturare qualche relazione tra l'area della figura trasformata e l'area della figura di partenza tenendo conto del valore del determinante?

Esperimento 2
Applica la trasformazione lineare individuata dalla matrice
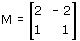

Ecco il codice di Derive

Insomma dovresti renderti conto che il determinante della matrice che caratterizza una trasformazione linerare ci fornisce delle utili informazioni sulla trasformazione stessa.

Esperimento 3
Le simmetrie rispetto agli assi cartesiani e rispetto all'origine sono trasformazioni del piano che ben conosci. Si tratta di trasformazioni lineari? Se sì, determinane le matrici e prova a trasformare delle figure.

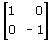
Si tratta in ogni caso di trasformazioni lineari. Le equazioni della simmetria rispetto all'asse delle x sono
x' = x
quindi si ha a=1, b=0, c=0, d=-1 e la matrice della trasformazione è
y' = -y
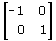
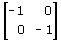

Esperimento 4
Si chiama punto unito (o fisso) di una trasformazione t ogni punto tale che t(P)=P cioè tale che non sia "mosso" dalla trasformazione. Verifica che una trasformazione lineare ha sempre l'origine come punto unito ma può avere altri punti uniti. Chiediti infine: le traslazioni del piano sono trasformazioni lineari?

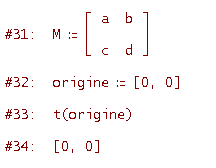
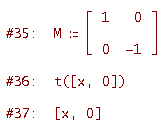
Osservazione 2 Una traslazione trasforma naturalmente rette in rette ma non è una trasformazione lineare perchè le sue equazioni
x' = x + p
y' = y + q

Esperimento 5
Esiste una trasformazione lineare che porti il quadrato di vertici [0, 0], [0, 1], [1, 1], [1, 0] nel parallelogramma di vertici [0, 0], [2, 2], [4, 2], [2, 0]?

Qui vedi le due figure
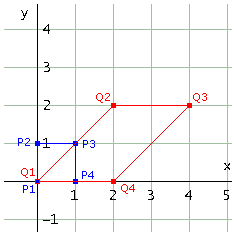

t(P3) = Q3
equivale a
[a·1 + b·1, c·1 + d·1] = [4, 2]
e quindi, dovendo coincidere sia le prime componenti sia le seconde, equivale alle due equazioni simultanee
a + b = 4
c + d = 2

Esperimento 6
Considera, utilizzando le solite equazioni, la corrispondenza di matrice
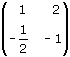




Esperimento 7
Considera la trasformazione lineare individuata dalla matrice
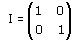

Proviamo a trasformare un generico punto [x, y]. Ecco il codice
