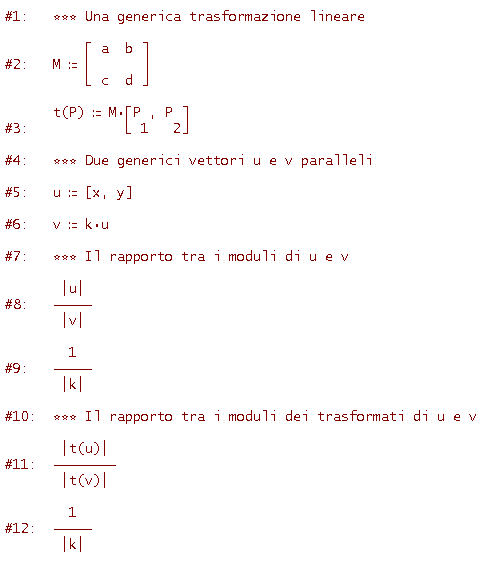Attività successiva
Attività precedente
Indice
Home

Attività 2 - Proprietà delle trasformazioni lineari del piano
Ogni punto [x, y] del piano può essere pensato come un vettore con punto iniziale nell'origine e punto finale in [x, y]. Possiamo quindi addizionare punti (cioè vettori) e moltiplicare punti (cioè vettori) per uno scalare (cioè per un numero reale k); ricorderai che, per definizione, si ha
Tieni presente che in seguito parleremo indifferentemente di vettori o di punti.
cioè il trasformato della somma di due vettori è la somma dei trasformati. Inoltre se k indica un numero reale si ha
cioè il trasformato del prodotto di un numero per un vettore è uguale al prodotto del numero per il trasformato del vettore. Ecco la dimostrazione con Derive
Semplificando le righe #6 e #8 si ottengono rispettivamente le righe #7 e #9, quindi lo stesso vettore; analogamente semplificando le righe #11 e #13 si ottiene lo stesso vettore.
Ricordando che Derive ci consente di operare con le equazioni, ci conviene chiamarle rispettivamente E1 ed E2
Poi opereremo così
Nota che alla riga #22 abbiamo moltiplicato la prima equazione per (c + dm), la seconda per (a + bm) e poi sottratto; si ottiene infine l'equazione della riga #25 che deve essere necessariamente soddisfatta dai punti trasformati [x1, y1]. Ora un'osservazione importante: i due numeri (c + dm) e (a + bm) non possono essere entrambi nulli perchè si avrebbe c = -dm, a = -bm e det(M) sarebbe nullo, contro l'ipotesi. Ne segue che l'equazione #25, che lega x1 e y1, è proprio l'equazione di una retta, come volevamo provare (proprietà 3). Ora, se (a + bm) è diverso da 0, procediamo così
Nota che in questo caso il coefficiente angolare della retta trasformata, chiamiamola r', è
e, come vedi, dipende dalla matrice M della trasformazione e dal coefficiente angolare m della retta di partenza ma non dipende da q. Ciò significa che se considerassimo una nuova retta s parallela ad r (quindi di stesso coefficiente angolare m) e applicassimo la stessa trasformazione di matrice M, otterremmo una retta s' parallela ad r'. Quindi, in questo caso, si conserva il parallelismo (proprietà 4). Esaminiamo ora il secondo caso possibile, cioè che sia a + bm = 0 e quindi, necessariamente, c + dm diverso da zero
Si ottiene una retta parallela all'asse delle y. Quindi, di nuovo, è verificata la proprietà 4. E' poi facile verificare le proprietà 3 e 4 nel caso in cui la retta di partenza sia parallela all'asse delle y cioè abbia equazione della forma x = k.
La verifica è immediata
Osservazione 2 Abbiamo visto che una trasformazione lineare trasforma rette in rette; sappiamo inoltre che una trasformazione lineare fissa l'origine (cioè ha l'origine come punto unito, vedi l'esperimento 4 dell'attività precedente). Si può dimostrare, viceversa, che ogni trasformazione del piano che muti rette in rette e fissi l'origine è una trasformazione lineare, cioè è definita dalle equazioni
al trapezio di vertici A=[1, 1], B=[2, 2], C=[3, 1], D=[1, -1]. Verifica che si conserva il rapporto tra i lati paralleli (cioè tra AB e CD) mentre non si conserva il rapporto tra i lati non paralleli. Dimostra, in generale, che una trasformazione lineare conserva il rapporto tra segmenti paralleli (o tra segmenti che si trovano sulla stessa retta).
[x, y] + [u, v] = [x+u, y+v]
e
k[x, y] = [kx, ky]
Mostriamo che se t è una trasformazione lineare del piano e [x, y] e [u, v] sono due generici vettori allora si ha
(proprietà 1) t([x, y] + [u, v]) = t([x, y]) + t([u, v])
(proprietà 2) t(k·[x, y]) = k·t([x, y])

Tieni presente che la riga #1 imposta la variabile di sistema CaseMode in modo che Derive distingua maiuscole da minuscole e quindi, ad esempio, distingua la variabile m dalla variabile M. Ci avvarremo di questa possibilità tra poco.
Osservazione 1 Abbiamo visto che ogni trasformazione lineare del piano verifica le proprietà 1 e 2. Si può dimostrare, viceversa, che se una trasformazione del piano verifica le proprietà 1 e 2 allora è una trasformazione lineare cioè è definita dalle equazioni
x' = ax + by
con ad - bc non nullo.
y' = cx + dy
Ora proveremo, in un sol colpo, due proprietà importanti che hai già intuito nell'attività precedente:
(proprietà 3) una trasformazione lineare trasforma rette in rette (ricorda che se M è la matrice della trasformazione deve essere det(M)
Ragioniamo così. I punti di una generica retta r di equazione y = mx + q (quindi non parallela all'asse delle y) sono della forma
 0);
0);
(proprietà 4) una trasformazione lineare trasforma rette parallele in rette parallele.
[x, mx+q]
Considerando i loro trasformati si ha
Quindi i punti trasformati, chiamiamoli [x1, y1], soddisfano le due equazioni

x1 = x(a + bm) + bq
y1 = x(c + dm) + dq
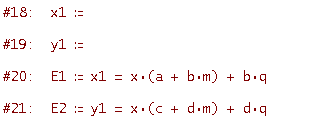

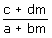

Ecco un'altra utile proprietà delle trasformazioni lineari:
(proprietà 5) una trasformazione lineare di matrice
trasforma il vettore [1, 0] nel vettore [a, c] e il vettore [0, 1] nel vettore [b, d] cioè trasforma i versori degli assi x e y rispettivamente nella prima e nella seconda colonna della matrice M.
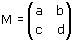

x' = ax + by
con ad - bc non nullo.
y' = cx + dy

Esperimento 1
Applica la trasformazione lineare individuata dalla matrice
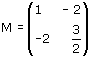

Ecco la figura e il codice di Derive
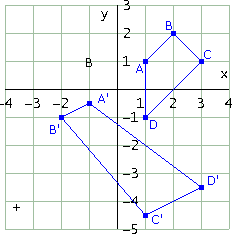
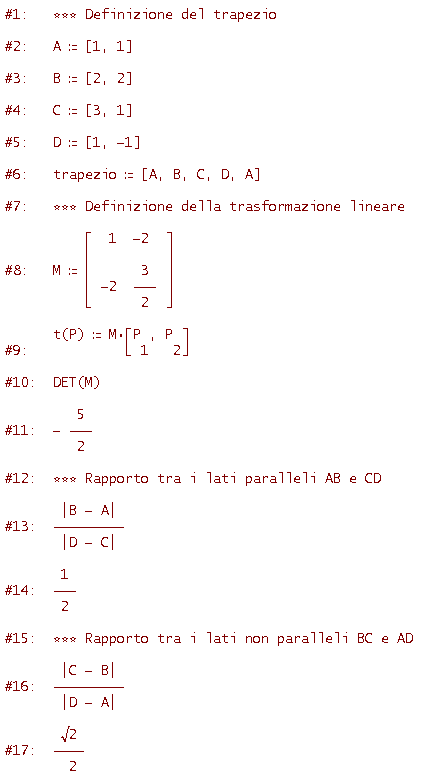
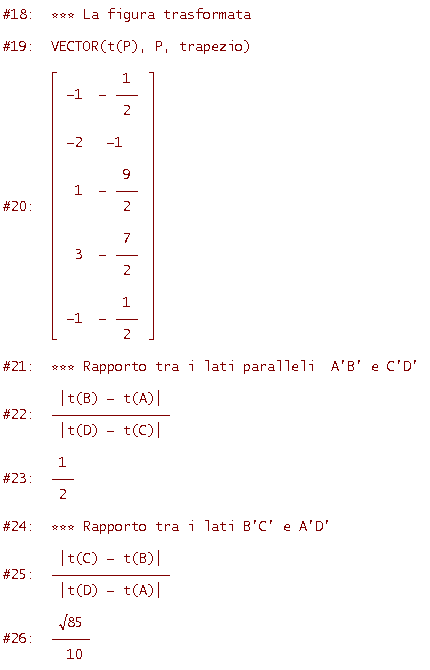
 Come vedi, le espressioni delle righe #13 e #22 forniscono lo stesso valore 1/2 e ciò prova che si conserva il rapporto dei lati paralleli.
Come vedi, le espressioni delle righe #13 e #22 forniscono lo stesso valore 1/2 e ciò prova che si conserva il rapporto dei lati paralleli.
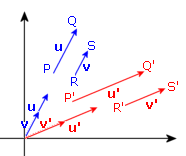
Per dimostrare in generale la proprietà verificata nel caso particolare del trapezio precedente, ci farà comodo formulare la questione in termini vettoriali. Siano PQ e RS due segmenti paralleli e P'Q', R'S' i loro trasformati (che sappiamo essere paralleli). Dire che i segmenti PQ e RS sono paralleli equivale a dire, indicando con u il vettore Q-P e con v il vettore S-R, che si ha v=ku (cioè v è un multiplo di u, k indica un numero reale). Ecco poi come procederemo
Dall'uguaglianza dei risultati alle righe #9 e #12 (rispettivamente semplificazioni delle righe #8 e #11) segue la tesi.