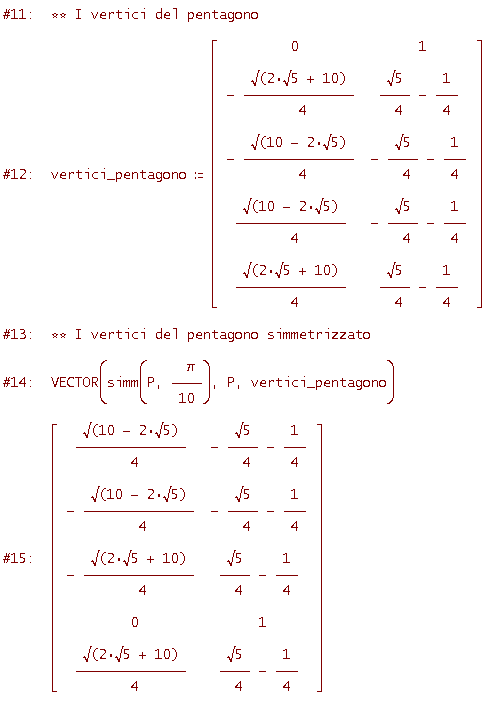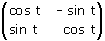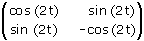Attività successiva
Attività precedente
Indice
Home

Attività 3 - Isometrie lineari
Un'isometria del piano è una trasformazione del piano che conserva le distanze (da cui segue, come è facile dimostrare, che trasforma rette in rette). Vogliamo determinare quali trasformazioni lineari siano isometrie (le chiameremo isometrie lineari). Condizione necessaria affinchè una trasformazione lineare sia un'isometria è che i versori degli assi [1, 0] e [0, 1], che hanno modulo unitario (cioè lunghezza 1), si trasformino in vettori di modulo 1 (perchè devono conservarsi le distanze); inoltre il vettore [1, 1] deve trasformarsi in un vettore di ugual modulo (per lo stesso motivo). Ricorda che il modulo di un vettore [x, y] è dato da
Una matrice quadrata M che verifichi le due condizioni precedenti si dice ortogonale. Proveremo tra poco che una matrice ortogonale ha sempre determinante non nullo (quindi la corrispondenza individuata da una matrice ortogonale è biunivoca, è cioè una trasformazione geometrica). Mostriamo che l'essere M una matrice ortogonale è condizione sufficiente (oltre che necessaria, come si è visto) affinchè la trasformazione lineare definita da M sia un'isometria. Basta dimostrare che si conserva il modulo di qualsiasi vettore; procedendo con Derive
Osserva che l'equazione della riga #16, ottenuta semplificando la #15, è verificata per ogni x e y essendo a2 + c2 = 1, b2 + d2 = 1 e ab + cd = 0.
Ora esaminiamo i due casi possibili d = -a oppure d = a, assumendo che a sia non nullo
Se infine a=0, si ha d=0; inoltre per la #23, b=±1 e per la #22, c=±1. In ogni caso dunque la matrice è del tipo indicato (ponendo A=a e B=c) e, per la #7, si ha A2 + B2 = 1.
Quindi, tenendo conto che A2 + B2 = 1, il determinate di una matrice ortogonale, cioè della matrice di un isometria lineare, è 1 oppure -1. Ciò è in accordo col fatto che un'isometria, conservando le distanze, conserva le aree (vedi l'esperimento 2 dell'attività 1). Osserva inoltre che se la matrice M è del tipo della riga #45 si tratta di un'isometria diretta, se è del tipo della riga #48 di un'isometria indiretta. Ricorda infatti che se il determinante di una trasformazione lineare è positivo allora si conserva l'orientamento (vedi l'esperimento 2 dell'attività 1) se è negativo si inverte l'orientamento.
Determina la matrice M della trasformazione lineare che ruota i versori degli assi di t radianti rispetto all'origine. Verifica che si tratta di un'isometria, più precisamente di una rotazione del piano attorno all'origine.
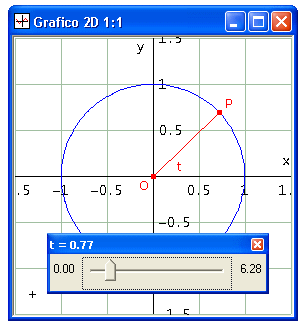
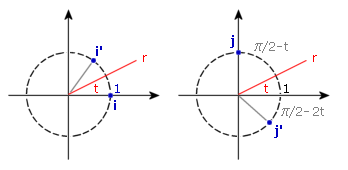
Un vettore OP di lunghezza unitaria ha la sua punta (cioè il vertice P) sulla circonferenza unitaria di equazione x2 + y2 = 1. Se il segmento OP forma un angolo di t radianti con l'asse delle x, le coordinate di P sono [cos t, sin t]. Ecco il foglio di lavoro
Inserisci, nella finestra grafica, una slider bar per il parametro t facendo variare t da 0 a 2PI (PI indica pigreco); poi traccia la rappresentazione grafica relativa alla righe #1 e #4. Otterrai la figura seguente ed agendo sul cursore della slider bar potrai ruotare il vettore OP (in senso antiorario al crescere di t).
Osserva che semplificando la riga #6, Derive mette la matrice M(t) nella forma più semplice della riga #7 (applicando le note formule trigonometriche per archi che differiscono di 90°). La riga #7 ci fa capire che la matrice M(t) è del tipo
con A2 + B2 = 1 e quindi si tratta della matrice di un isometria. Poichè si ha det(M)=1 per ogni t, si tratta di un isometria diretta; ne segue che la trasformazione è necessariamente una rotazione del piano attorno all'origine, tenendo conto che l'origine è un punto fisso (qui devi ricordare che le isometrie dirette del piano sono rotazioni o traslazioni e che una traslazione di componenti non entrambe nulle non ha punti uniti).
(considereremo anche la rotazione nulla e quella di un angolo giro per ottenere all'inizio e alla fine il punto P). Ecco il codice
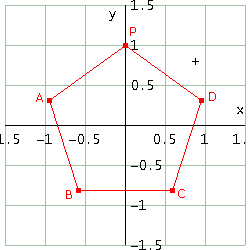
Tracciando la rappresentazione grafica della riga #12 (semplificazione della #11) ottieni il pentagono regolare della figura seguente
Osservazione 1 Abbiamo dunque visto che la matrice di una rotazione attorno all'origine è del tipo
con A2 + B2 = 1.
Determina la matrice M della trasformazione lineare che ribalta i versori degli assi rispetto alla retta r passante per l'origine e formante un angolo di t radianti con l'asse delle x. Verifica che si tratta di un'isometria, più precisamente di una simmetria rispetto alla retta r.
Tenendo conto delle figure precedenti e della proprietà 5 delle trasformazioni lineari esaminata nell'attività precedente è facile determinare la matrice M:
La matrice M(t) è, come vedi, del tipo
Verifichiamo che si tratta della matrice di un'isometria indiretta e quindi, ricordando che le isometrie indirette del piano sono simmetrie o antitraslazioni (e che queste ultime non hanno punti uniti), si tratta necessariamente di una simmetria rispetto alla retta r
Proviamo il nostro comando simm(P, t). A titolo d'esempio consideriamo il pentagono regolare dell'esempio precedente (vai a rivedere la figura) e verifichiamo che torna su se stesso mediante una simmetria rispetto alla retta per l'origine e per il punto D (naturalmente si avrà una permutazione dei vertici). Tale retta forma evidentemente un angolo di
Confrontando le coordinate alle righe #12 e #15, ti rendi conto che ogni vertice del pentagono è trasformato in un altro vertice del pentagono e quindi la figura torna su se stessa.
cioè è la lunghezza del segmento dall'origine al punto [x, y]. Ecco il foglio di Derive
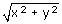
Tenendo conto delle condizioni #7 e #9, la condizione #11 diventa

Interpretando geometricamente queste condizioni possiamo dire che
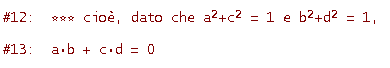

Mostriamo ora che una matrice ortogonale 2x2 è del tipo
con A2 + B2 = 1. Ecco il codice

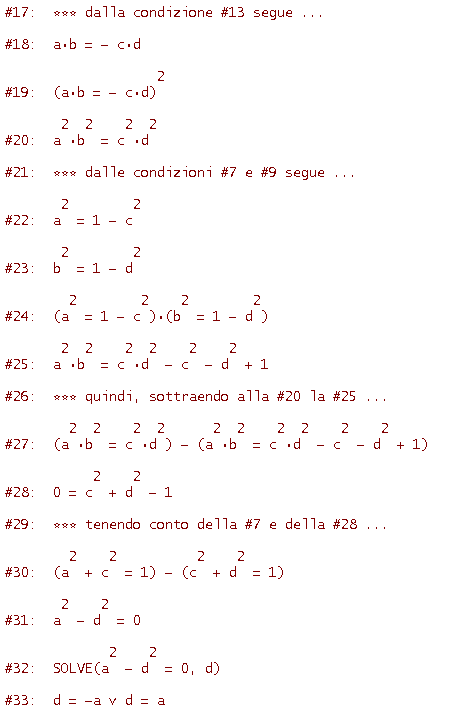

Calcoliamo il determinante di una matrice ortogonale
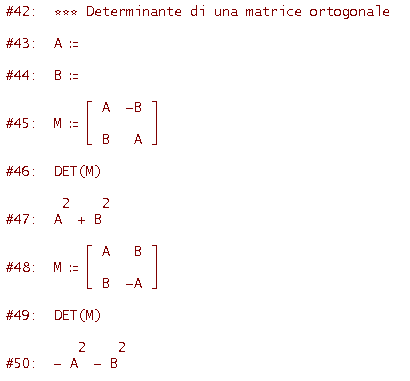

Esperimento 1

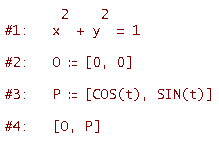
Ora è facile determinare la matrice M grazie alla proprietà 5 delle trasformazioni lineari esaminata nell'attività precedente:
Ecco il codice
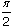 + t), sin(
+ t), sin(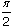 + t)] (seconda colonna di M).
+ t)] (seconda colonna di M).
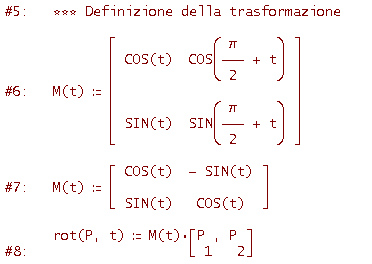
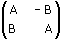
E' il momento di mettere alla prova il nostro comando rot(P, t). A titolo d'esempio costruiamo un pentagono regolare ruotando il punto P = [0, 1] rispetto all'origine di
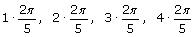
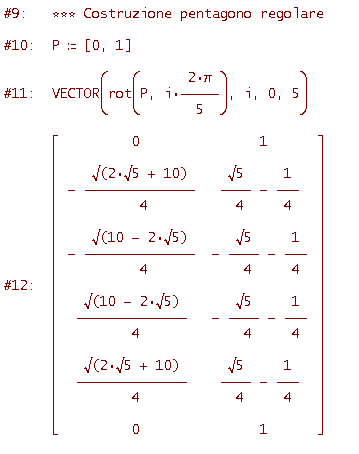
Visto che ci siamo, è anche facile calcolare la lunghezza del lato del pentagono (è il modulo del vettore PA) e la lunghezza della diagonale (è il modulo del vettore AC); potremo così verificare che il rapporto tra le due misure è la sezione aurea. Ecco il codice
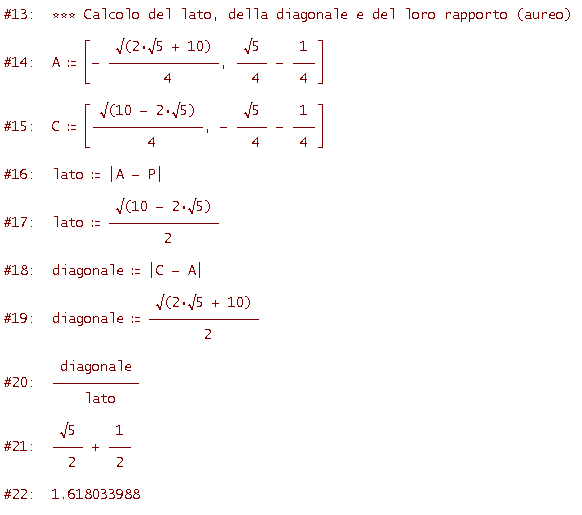
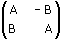

Esperimento 2

Ecco il codice
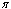 -(
-(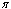 /2-2t)), sin(2
/2-2t)), sin(2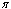 -(
-(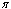 /2-2t))] =
/2-2t))] =
= [sin(2t), -cos(2t)] (seconda colonna di M).

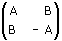

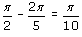 radianti con l'asse delle x. Ecco il codice
radianti con l'asse delle x. Ecco il codice