Attività successiva
Attività precedente
Indice
Home

Attività 5 - Altre trasformazioni lineari: stiramenti e scorrimenti
Esaminiamo altre importanti trasformazioni lineari (scrivi tu il codice per implementarle con Derive: se sei arrivato sin qui sarà facile).
Come vedi, se gli stiramenti rispetto ai due assi hanno lo stesso coefficiente, cioè a=b, si ottiene un'omotetia con centro nell'origine (vedi l'esperimento 3 dell'attività precedente).
Ora fai tu degli esperimenti. Gli scorrimenti conservano l'area di una figura? Ragiona sia algebricamente (cioè sulla matrice), sia geometricamente. In che modo uno stiramento modifica l'area di una figura?
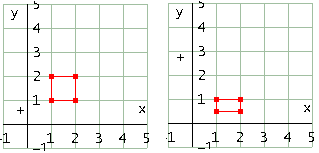
Matrice
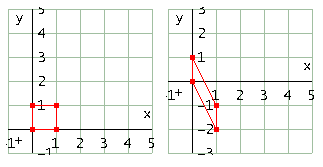
Effetto sul quadrato in figura con a=2
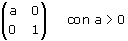
Effetto sul quadrato in figura con a=1/2
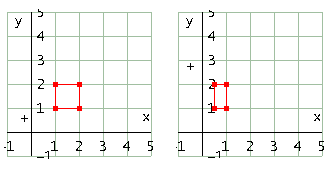
Matrice
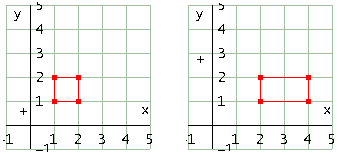
Effetto sul quadrato in figura con b=2

Effetto sul quadrato in figura con b=1/2
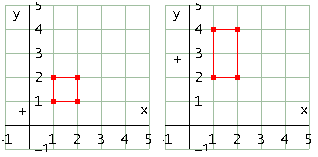
Matrice
Effetto sul quadrato in figura con a=2 e b=3/2

Effetto sul quadrato in figura con a=2 e b=2
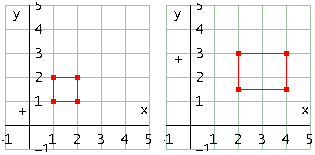
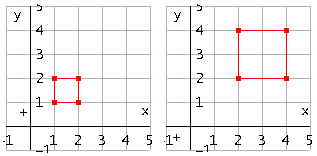
Matrice
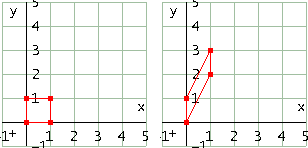
Effetto sul quadrato in figura con a=2
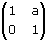
Effetto sul quadrato in figura con a=-2
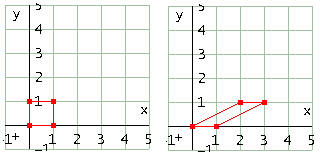
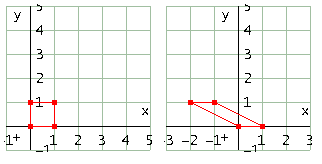
Matrice
Effetto sul quadrato in figura con a=2
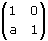
Effetto sul quadrato in figura con a=-2