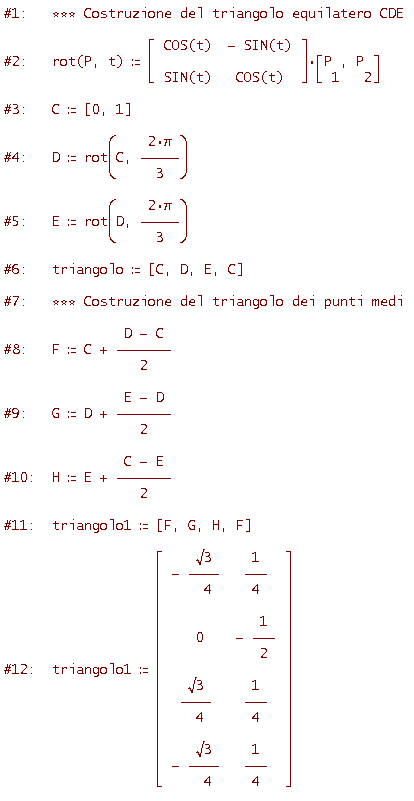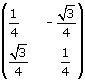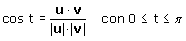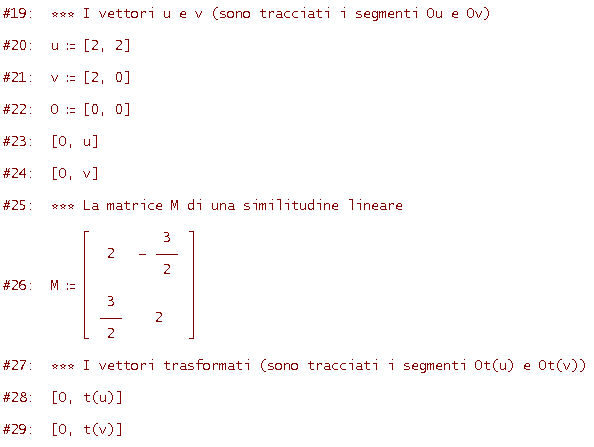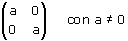Attività successiva
Attività precedente
Indice
Home
Attività 4 - Similitudini lineari
In questa attività vogliamo individuare le trasformazioni lineari del piano che conservano la forma delle figure cioè che sono similitudini: le chiameremo similitudini lineari. In generale, come sai, una similitudine è una trasformazione del piano che trasforma rette in rette e conserva gli angoli e il rapporto di segmenti. E' facile dimostrare, utilizzando i criteri di similitudine, che le due proprietà sono equivalenti cioè una trasformazione del piano che trasformi rette in rette conserva gli angoli se e solo se conserva il rapporto di segmenti.
con det(M) non nullo allora la trasformazione è una similitudine. Fai attenzione: si tratta dello stesso tipo di matrici che caratterizzano le isometrie lineari ma qui non si pone la condizione che sia A2 + B2 = 1.
Come vedi, i rapporti delle righe #8 e #10 (semplificati rispettivamente nei rapporti #9 e #11) sono uguali; analogamente lo sono i rapporti delle righe #15 e #17. Ciò significa che le matrici succitate individuano una similitudine. Si può inoltre dimostrare che, viceversa, ogni trasformazione lineare che sia una similitudine ha una matrice del tipo
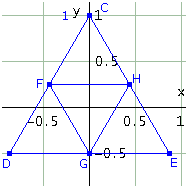
Costruisci un triangolo equilatero CDE, collega poi i punti medi dei lati ottenendo un secondo triangolo equilatero FGH. Determina la matrice della similitudine lineare che trasforma il primo nel secondo.
Mostriamo che se la matrice M di una trasformazione lineare è del tipo
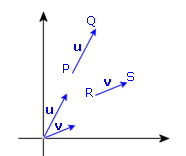Mostreremo che si conserva il rapporto di due generici segmenti PQ ed RS, cioè si conserva il rapporto tra i moduli dei due vettori u=Q-P e v=S-R. Ecco il codice di Derive
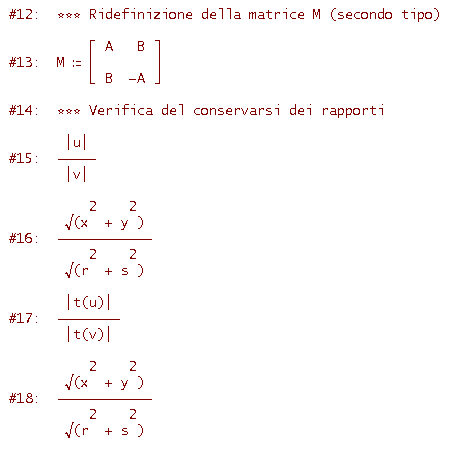
con det(M) non nullo (condizione di biunivocità).
Osservazione
In ogni caso il valore assoluto del determinante è A2 + B2. Ciò significa che se F è una figura e F' la sua trasformata allora
allora det(M) = A2 + B2 è un numero positivo (poichè si esclude che sia nullo) e quindi si conserva l'orientamento delle figure; parleremo in questo caso di similitudine lineare diretta.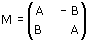
allora det(M) = -A2 -B2 è un numero negativo (poichè si esclude che sia nullo) e quindi si inverte l'orientamento delle figure; parleremo in questo caso di similitudine lineare indiretta.
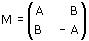
area(F')=|det(M)|·area(F)
(vedi l'esperimento 2 dell'attività 1) e quindi, ricordando che il rapporto tra le aree di figure simili è uguale al quadrato del rapporto di similitudine, si ha
rapporto di similitudine =
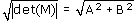
Esperimento 1
Ecco il codice di Derive
Osservando la figura si capisce che la similitudine è diretta (perchè si conserva l'orientamento) e quindi nella riga #14 in cui si definisce la trasformazione si è scelta la matrice del primo tipo. In conclusione la matrice cercata è
Come vedi, il suo determinante è 1/4, in accordo col fatto che il rapporto di similitudine è evidentemente 1/2.
Esperimento 2
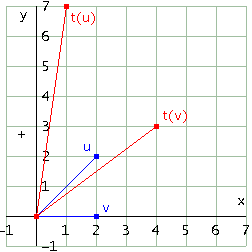
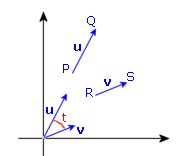
Mostra che una similitudine lineare conserva gli angoli, ricordando che l'angolo t tra due vettori u e v è individuato mediante la formula
Ecco il codice
Esaminiamo un caso concreto, tracciando determinati vettori u, v e i trasformati t(u) e t(v) per una determinata similitudine lineare (vedi figura seguente).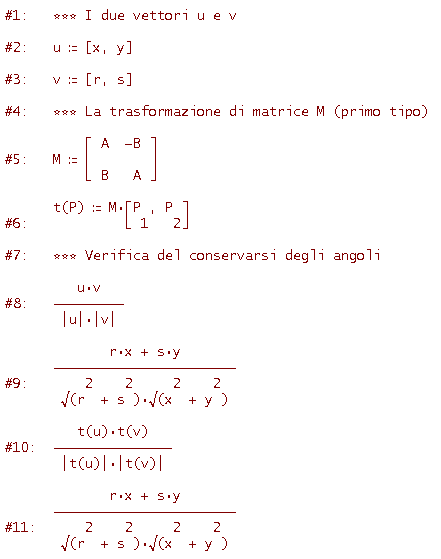
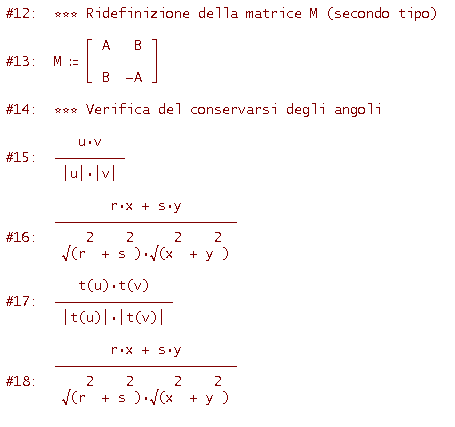
Esperimento 3
Verifica che una similitudine lineare la cui matrice sia del tipo
conserva la direzione cioè trasforma una qualsiasi retta r in una retta r' parallela ad r (o coincidente con r). Tali similitudini prendono il nome di omotetie col centro nell'origine e sono similitudini dirette (perchè?).
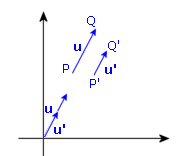Poichè sappiamo che qualsiasi trasformazione lineare trasforma rette in rette, basta mostrare che un generico segmento PQ si trasforma in un segmento P'Q' parallelo a PQ cioè, equivalentemente, che il vettore u = Q-P si trasforma in un vettore u' tale che u'=ku (con k numero reale non nullo). Ecco il codice
