Attività successiva
Attività precedente
Indice
Home

Attività 6 - Trasformazioni affini
dove
sono rispettivamente la matrice e il vettore della trasformazione affine.
L'effetto geometrico di una trasformazione affine è determinato, a meno di una traslazione, dall'effetto prodotto da una trasformazione lineare.
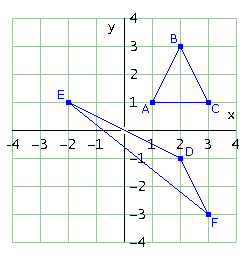
Traccia nel piano due triangoli qualsiasi ABC e DEF. Verifica che esiste una e una sola trasformazione affine che muta il triangolo ABC nel triangolo DEF.
 Sappiamo che le trasformazioni lineari del piano sono le trasformazioni che mutano rette in rette e fissano l'origine (vedi l'osservazione 2 dell'attività 2). D'altra parte una trasformazione
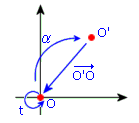
Sappiamo che le trasformazioni lineari del piano sono le trasformazioni che mutano rette in rette e fissano l'origine (vedi l'osservazione 2 dell'attività 2). D'altra parte una trasformazione  del piano che muti rette in rette e non fissi l'origine (quindi che porti l'origine O in un punto O'), può essere ricondotta ad una trasformazione lineare t: basta comporre
del piano che muti rette in rette e non fissi l'origine (quindi che porti l'origine O in un punto O'), può essere ricondotta ad una trasformazione lineare t: basta comporre  con la traslazione di vettore O'O (che porta O' in O). Infatti eseguendo di seguito
con la traslazione di vettore O'O (che porta O' in O). Infatti eseguendo di seguito  e la traslazione di vettore O'O si ottiene una trasformazione che muta rette in rette (perchè così fanno sia
e la traslazione di vettore O'O si ottiene una trasformazione che muta rette in rette (perchè così fanno sia  sia la traslazione) e che fissa l'origine. Ne segue che una qualsiasi trasformazione del piano
sia la traslazione) e che fissa l'origine. Ne segue che una qualsiasi trasformazione del piano  che muti rette in rette si ottiene componendo una trasformazione lineare e una traslazione (precisamente componendo la trasformazione lineare t con la traslazione di vettore OO').
che muti rette in rette si ottiene componendo una trasformazione lineare e una traslazione (precisamente componendo la trasformazione lineare t con la traslazione di vettore OO').
Chiameremo trasformazione affine una qualsiasi trasformazione del piano che muti rette in rette; ci siamo allora resi conto che una trasformazione affine si ottiene componendo una trasformazione lineare con una traslazione perciò le sue equazioni sono
x' = ax + by + p
o, in forma matriciale,
y' = cx + dy + q
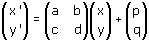
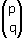 è il vettore che individua la traslazione, ovvero p e q sono rispettivamente le componenti orizzontale e verticale della traslazione. Diremo che la matrice
è il vettore che individua la traslazione, ovvero p e q sono rispettivamente le componenti orizzontale e verticale della traslazione. Diremo che la matrice
e il vettore
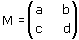
v =
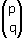

Esperimento 1

Ecco il codice:
Osservazione 1 In generale si può dimostrare il seguente teorema fondamentale sulle trasformazioni affini: se A, B, C e D, E, F sono due gruppi di tre punti non allineati del piano (se cioè individuano due triangoli) allora esiste una e una sola trasformazione affine che porta i punti A, B, C rispettivamente nei punti D, E, F.
Osservazione 2 Diremo che due figure del piano sono affini se esiste una trasformazione affine che muti l'una nell'altra. Tenendo conto dell'esempio 1 e dell'osservazione 1, ti rendi conto che tutti i triangoli del piano sono affini. Non è vero invece che tutti i quadrilateri del piano siano affini mentre è vero che lo sono tutti i parallelogrammi (fai qualche esperimento).

Esperimento 2
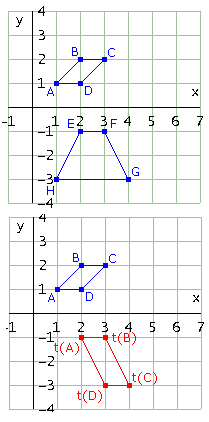
Esiste una trasformazione affine che muti il parallelogramma di vertici A=[1, 1], B=[2, 2], C=[3, 2], D=[2, 1] nel trapezio di vertici E=[2, -1], F=[3, -1], G=[4, -3], H=[1, -3]? Fai degli esperimenti e discuti la questione.

Ecco figure e codice
Si potrebbe dire subito che non esiste una trasformazione affine che muti un parallelogramma in un trapezio perchè una trasformazione affine conserva il parallelismo (essendo ottenuta per composizione di una trasformazione lineare che, lo sappiamo, conserva il parallelismo e di una traslazione che evidentemente conserva il parallelismo). Osserviamo inoltre che esiste una e una sola trasformazione affine che porti i punti A, B, C rispettivamente nei punti E, F, G (vedi l'osservazione 1); il trasformato del punto D è poi "obbligato" a completare un parallelogramma, dovendosi conservare il parallelismo e il rapporto tra segmenti paralleli (i segmenti AB e CD sono paralleli e hanno rapporto 1 e tali devono esserlo i segmenti trasformati).
Osservazione 3 Le trasformazioni affini, ottenendosi per composizione di una trasformazione lineare e di una traslazione, conservano il parallelismo. Tutti i parallelogrammi sono affini ma non lo sono tutti i quadrilateri.