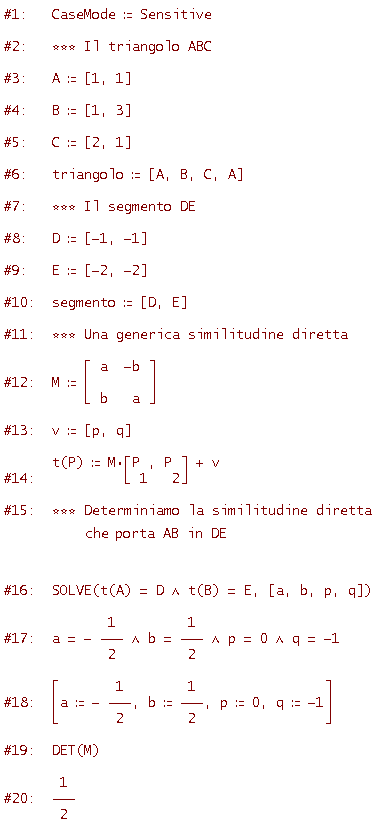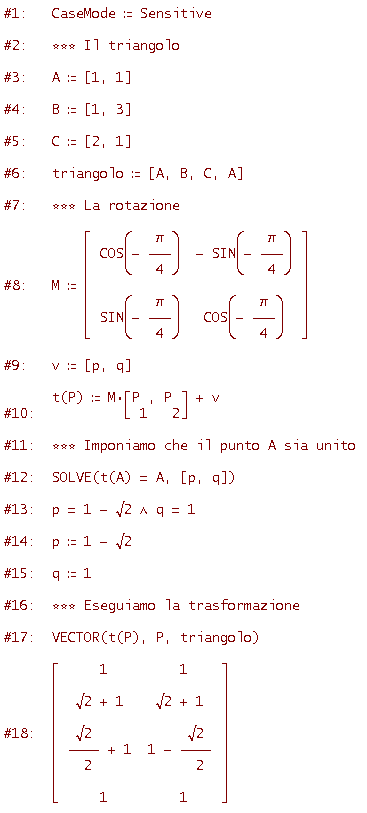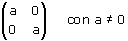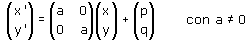Attività successiva
Attività precedente
Indice
Home

Attività 7 - Isometrie e similitudini
Nell'attività 3 abbiamo studiato le isometrie lineari cioè le isometrie che fissano l'origine. In generale, però, un'isometria non lascia fissa l'origine: vogliamo ora occuparci del caso generale. Un'isometria trasforma naturalmente rette in rette ed è quindi un caso particolare di trasformazione affine. D'altra parte una trasformazione affine, lo sappiamo, si ottiene componendo una trasformazione lineare t e una traslazione; ora, affinchè una trasformazione affine conservi le distanze, è evidentemente necessario (e sufficiente) che le conservi la trasformazione t. E ciò significa che la matrice M della trasformazione t deve essere ortogonale. Siamo dunque in grado di enunciare un teorema fondamentale sulle isometrie del piano: ogni isometria del piano è una trasformazione della forma
dove la matrice
Nel primo caso si tratta di una rotazione attorno all'origine di un angolo
con a2+b2 non nullo. Nel primo caso la similitudine è diretta, nel secondo indiretta.
Considera il triangolo ABC con A=[1, 1], B=[1, 3], C=[2, 1] e il triangolo DEF con D=[-1, -2], E=[-3, -2], F=[-1, -3]. Determina la trasformazione affine che muta il primo nel secondo e verifica che si tratta di un'isometria indiretta.
x' = ax + by + p
o, equivalentemente, della forma
y' = cx + dy + q
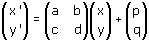
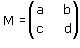 è ortogonale. Tenendo conto dell'osservazione 2 dell'attività 3, rimane anche dimostrato che un'isometria del piano è della forma
è ortogonale. Tenendo conto dell'osservazione 2 dell'attività 3, rimane anche dimostrato che un'isometria del piano è della forma
oppure della forma
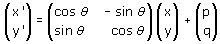
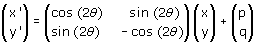
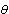 seguita da una traslazione di vettore [p, q]; nel secondo caso di una simmetria rispetto ad una retta per l'origine formante un angolo
seguita da una traslazione di vettore [p, q]; nel secondo caso di una simmetria rispetto ad una retta per l'origine formante un angolo 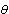 con l'asse delle x seguita dalla solita traslazione di vettore [p, q]. Nel primo caso l'isometria è diretta e si ha det(M)=1, nel secondo l'isometria è indiretta e si ha det(M)=-1.
con l'asse delle x seguita dalla solita traslazione di vettore [p, q]. Nel primo caso l'isometria è diretta e si ha det(M)=1, nel secondo l'isometria è indiretta e si ha det(M)=-1.
Un discorso del tutto analogo può farsi per le similitudini. Nell'attività 4 abbiamo studiato le similitudini lineari cioè le similitudini che fissano l'origine. In generale, però, una similitudine non lascia fissa l'origine. Poichè le similitudini trasformano rette in rette anche le similitudini sono particolari trasformazioni affini. Ti rendi conto inoltre che condizione necessaria e sufficiente affinchè una trasformazione affine, ottenuta per composizione di una trasformazione lineare t e di una traslazione, sia una similitudine è che lo sia la trasformazione lineare t. Ricordando quanto visto nell'attività 4
si ha quindi che l'equazione di una similitudine del piano è della forma
oppure della forma
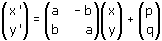
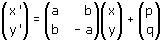

Esperimento 1

Ecco figura e codice
Abbiamo dunque individuato la trasformazione: la matrice è M (riga #26) e il vettore v=[0, -1]. Poichè si tratta di un'isometria indiretta le sue equazioni sono



e quindi cos(2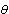 )=0 e sin(2
)=0 e sin(2 )=-1, da cui segue 2
)=-1, da cui segue 2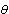 =3
=3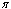 /2,
/2, 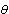 =3
=3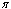 /4. Ti rendi conto allora che l'isometria consiste in una simmetria rispetto alla bisettrice del secondo e quarto quadrante seguita dalla traslazione verticale di una unità verso il basso (perchè p=0 e q=-1).
/4. Ti rendi conto allora che l'isometria consiste in una simmetria rispetto alla bisettrice del secondo e quarto quadrante seguita dalla traslazione verticale di una unità verso il basso (perchè p=0 e q=-1).
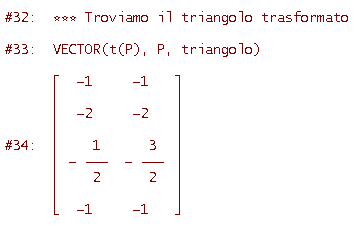
Nota che alle righe #29 e #31 abbiamo utilizzato l'operatore COL che serve ad estrarre una colonna da una matrice (nel nostro caso rispettivamente la prima e la seconda colonna); è allora facile verificare che la matrice M è ortogonale perchè i vettori colonna hanno modulo 1 e il loro prodotto scalare è nullo.

Esperimento 2
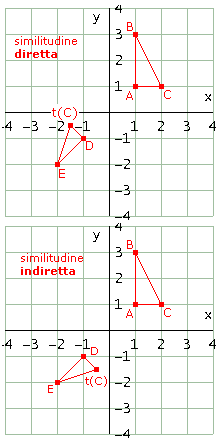
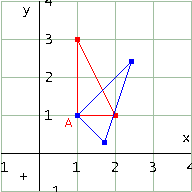
Considera il triangolo ABC con A=[1, 1], B=[1, 3], C=[2, 1] e un segmento DE a tuo piacere. Trasforma per similitudine il triangolo in modo che il lato AB vada in DE. Hai una sola possibilità?

Ci sono due possibilità: trasformare il triangolo mediante una similitudine diretta oppure indiretta. Ecco figure e codice
Osserva che i due possibili triangoli trasformati sono simmetrici rispetto al lato DE, come era da aspettarsi.

Esperimento 3
Considera il solito triangolo ABC con A=[1, 1], B=[1, 3], C=[2, 1]. Ruota il triangolo di 45° gradi in senso orario attorno al vertice A.

Qui, attento, abbiamo una rotazione rispetto ad un punto A diverso dall'origine. Poichè una rotazione rispetto ad un punto diverso dall'origine equivale ad una rotazione rispetto all'origine (di stessa ampiezza) seguita da un'opportuna traslazione, l'equazione matriciale della trasformazione è
(se non sei convinto vai a vedere l'attività con Cabri Rotazioni del piano: una proprietà).
Nel nostro caso si ha 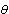 =-
=-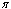 /4, dobbiamo determinare il vettore v=[p, q]. Per determinare v sfrutteremo il fatto che il punto A deve essere unito. Ecco codice e figure
/4, dobbiamo determinare il vettore v=[p, q]. Per determinare v sfrutteremo il fatto che il punto A deve essere unito. Ecco codice e figure

Esperimento 4
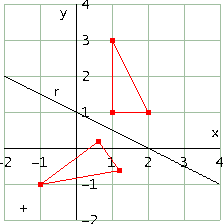
Considera il solito triangolo ABC con A=[1, 1], B=[1, 3], C=[2, 1]. Simmetrizza il triangolo rispetto alla retta r di equazione y=-1/2x+1.

Qui, attento, abbiamo una simmetria rispetto ad una retta non passante per l'origine. Poichè la simmetria rispetto ad una retta r non passante per l'origine equivale alla simmetria rispetto alla retta r' parallela ad r e passante per l'origine seguita da un'opportuna traslazione, l'equazione matriciale della trasformazione è
(se non sei convinto vai a vedere l'attività con Cabri Simmetrie assiali: una proprietà).
Nel nostro caso si ha 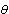 =atan(-1/2), dobbiamo determinare il vettore v=[p, q]. Per determinare v sfrutteremo il fatto che un punto qualsiasi di r deve essere unito, ad esempio il punto [0, 1]. Ecco codice e figure
=atan(-1/2), dobbiamo determinare il vettore v=[p, q]. Per determinare v sfrutteremo il fatto che un punto qualsiasi di r deve essere unito, ad esempio il punto [0, 1]. Ecco codice e figure

Esperimento 5
Nell'esperimento 3 dell'attività 4 hai verificato che una similitudine lineare t di matrice
conserva la direzione cioè trasforma una qualsiasi retta r in una retta r' parallela ad r o coincidente con r. Ne segue che anche una similitudine di equazione
conserva la direzione perchè ottenuta componendo t con una traslazione (come sai, le traslazioni conservano la direzione e componendo due trasformazioni che conservano la direzione si ottiene, evidentemente, una trasformazione che conserva la direzione). Dimostra che una trasformazione di questo tipo ha, se a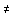 1, uno e un solo punto unito. Qual è il significato geometrico del punto unito? Fai degli esperimenti.
1, uno e un solo punto unito. Qual è il significato geometrico del punto unito? Fai degli esperimenti.

Ecco il codice
Osserva che, dopo aver definito la similitudine s(P), si cerca la soluzione dell'equazione vettoriale lineare s(P)=P in cui l'incognita è il vettore P=[x, y]. Se a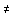 1, la soluzione esiste ed è unica (riga #8). Se invece a=1, la similitudine s(P) si riduce alla traslazione di vettore v e non ha quindi punti uniti a meno che non sia v = [p, q] = [0, 0] nel qual caso si ha la trasformazione identica per cui ogni punto del piano è punto unito (vedi l'esperimento 7 dell'attività 1).
1, la soluzione esiste ed è unica (riga #8). Se invece a=1, la similitudine s(P) si riduce alla traslazione di vettore v e non ha quindi punti uniti a meno che non sia v = [p, q] = [0, 0] nel qual caso si ha la trasformazione identica per cui ogni punto del piano è punto unito (vedi l'esperimento 7 dell'attività 1).
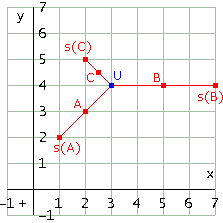
Ora facciamo qualche esperimento per capire qual è il significato geometrico del punto unito. Fissiamo il valore di a, cioè del rapporto di similitudine (vedi l'osservazione dell'attività 4), poniamo ad esempio a = 2; imponiamo poi che il punto unito della trasformazione sia un punto determinato, ad esempio il punto U = [3, 4]; trasformiamo quindi alcuni punti scelti a piacere e osserviamo le rappresentazioni grafiche. Ecco codice e figura
Ti rendi conto che comunque si scelga il punto A (purchè non coincida con U), i punti U, A e s(A) sono allineati, inoltre la distanza di s(A) da U è uguale a 2 volte la distanza di A da U.
Una trasformazione di questo tipo prende il nome di omotetia di rapporto a e centro U.
Fai altri esperimenti variando il valore di a. I casi da esaminare sono i seguenti: a > 1 (appena esaminato), a = 1 (traslazione o trasformazione identica), 0 < a < 1, -1 < a < 0, a < -1. Non dimenticare che il caso a=0 va escluso perchè non avremmo una corrispondenza biunivoca.
In generale, in un omotetia (non identica) di rapporto a e centro U, comunque si scelga un punto P diverso dal centro
- il punto P e il suo trasformato P' sono allineati con il centro U (se a > 0, P' si trova dalla stessa parte di P rispetto a U, se a < 0, P' si trova dalla parte opposta di P rispetto ad U);
- distanza(P', U) = |a|·distanza(P, U)
cioè la distanza di P' da U è uguale al modulo di a per la distanza di P da U.