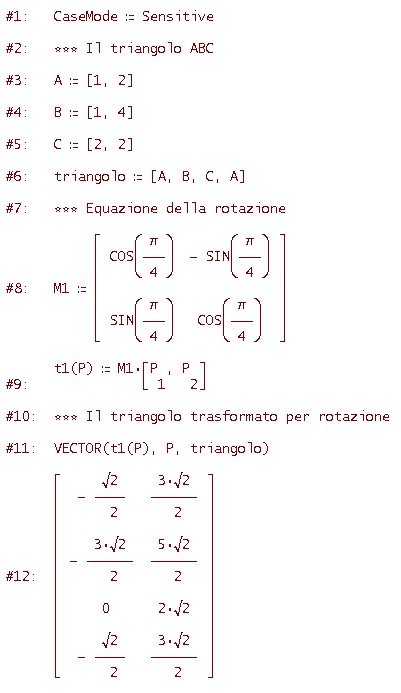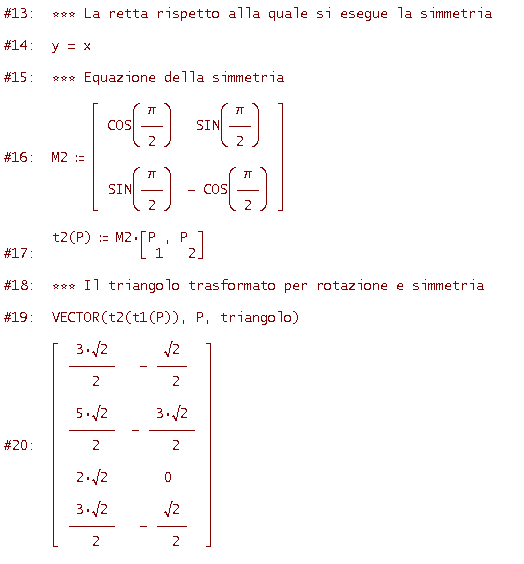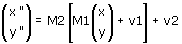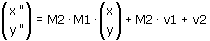Attività successiva
Attività precedente
Indice
Home

Attività 8 - Prodotto di trasformazioni
Come sai, la trasformazione t3 che porta [x, y] in [x", y"] si chiama prodotto o composizione delle due trasformazioni t2 e t1 e si scrive
Mostriamo che il prodotto di due trasformazioni lineari t2 e t1 è ancora una trasformazione lineare e, se B ed A sono rispettivamente le matrici di t2 e t1 allora la matrice BA, prodotto delle due matrici, è la matrice della trasformazione prodotto t2t1 (questo fatto, per inciso, è un buon motivo per giustificare l'usuale definizione di prodotto tra matrici). Ecco il codice
Verifichiamo che, essendo per ipotesi A e B due matrici a determinante non nullo, la matrice C ha anch'essa determinante non nullo e quindi la funzione composta è effettivamente una trasformazione geometrica (condizione di biunivocità); ciò segue dal fatto che il determinante del prodotto di due matrici è uguale al prodotto dei determinanti. Ecco il codice
Osservazione Abbiamo dunque mostrato per via algebrica che componendo due trasformazioni lineari si ottiene ancora una trasformazione lineare. Ma che le cose stiano così lo si poteva capire, immediatamente, per via geometrica. E' chiaro infatti che il prodotto di due trasformazioni è ancora una trasformazione (perchè il prodotto di corrispondenze biunivoche è ancora una corrispondenza biunivoca) e che il prodotto di due trasformazioni che mutano rette in rette e fissano l'origine è ancora una trasformazione che muta rette in rette e fissa l'origine. Rifletti.
Considera il triangolo ABC con A=[1, 2], B=[1, 4], C=[2, 2]. Applica al triangolo la trasformazione ottenuta componendo nell'ordine una rotazione antioraria di 45° rispetto all'origine e una simmetria rispetto alla retta di equazione y=x. Applica quindi le trasformazioni in ordine inverso, cioè prima la simmetria e poi la rotazione: ottieni la stessa trasformazione composta? (Vale, cioè, la proprietà commutativa per il prodotto di trasformazioni?)
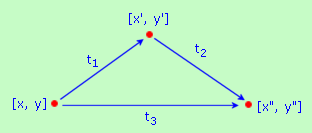 Se t1 e t2 sono due trasformazioni, possiamo eseguirle una di seguito all'altra (prima t1 e poi t2) ottenendo così una nuova trasformazione t3; se t1 porta il punto [x, y] nel punto [x', y'] e t2 porta il punto [x', y'] nel punto [x", y"] allora t3 porta "direttamente" il punto [x, y] nel punto [x", y"]. Quindi
Se t1 e t2 sono due trasformazioni, possiamo eseguirle una di seguito all'altra (prima t1 e poi t2) ottenendo così una nuova trasformazione t3; se t1 porta il punto [x, y] nel punto [x', y'] e t2 porta il punto [x', y'] nel punto [x", y"] allora t3 porta "direttamente" il punto [x, y] nel punto [x", y"]. Quindi
t3([x, y]) = t2(t1([x, y])) = [x", y"]
t3 = t2t1
(leggi: t3 uguale a t2 per t1).
Verifichiamo che la matrice C è il prodotto (righe per colonne) delle matrici B ed A




Esperimento 1

Ecco codice e figura (il triangolo rosso è quello di partenza, quello azzurro è il trasformato per rotazione, quello rosa è il trasformato per rotazione e simmetria)
Nota che la retta di equazione y=x forma con l'asse delle x un angolo di 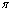 /4 radianti e quindi la matrice della trasformazione è
/4 radianti e quindi la matrice della trasformazione è
(vedi l'osservazione 2 dell'attività 3).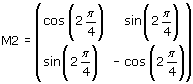
Tieni presente inoltre che la matrice della trasformazione composta (simmetria per rotazione cioè prima la rotazione poi la simmetria) è
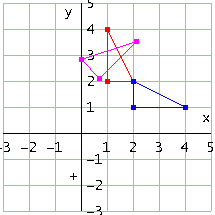
Ora eseguiamo le trasformazioni in ordine inverso
In figura vedi il triangolo ABC (quello rosso), il triangolo ABC trasformato per simmetria (quello azzurro), il triangolo ABC trasformato applicando prima la simmetria e poi la rotazione (quello rosa). La trasformazione composta rotazione per simmetria non è dunque equivalente alla trasformazione composta simmetria per rotazione: non vale (in generale) la proprietà commutativa. Ne hai la conferma confrontando la matrice della nuova trasformazione composta con la matrice della riga #23
(Con ciò ti rendi conto che pure per il prodotto di matrici non vale in generale la proprietà commutativa. Puoi pensare, geometricamente, al prodotto di matrici come al prodotto di trasformazioni lineari.)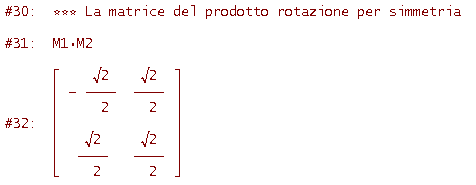

Esperimento 2
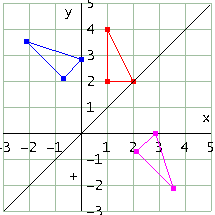
Considera il solito triangolo ABC con A=[1, 2], B=[1, 4], C=[2, 2]. Applica al triangolo la trasformazione ottenuta componendo nell'ordine una rotazione antioraria di 45° rispetto al punto C e una simmetria rispetto alla nuova posizione del lato BC.

Fai attenzione, qui entrano in gioco una rotazione rispetto a un punto diverso dall'origine e una simmetria rispetto a una retta non passante per l'origine; le equazioni delle trasformazioni (isometrie) sono quindi quelle esaminate nell'attività 7. Ti rendi conto inoltre, geometricamente, che la trasformazione composta di una rotazione e di una simmetria sarà un'isometria indiretta (perciò la matrice della trasformazione composta avrà determinante uguale a -1).
Ecco codice e figura (il triangolo rosso è quello di partenza, quello azzurro è il trasformato per rotazione, quello rosa è il trasformato per rotazione e simmetria)
Tieni presente che la riga #28 non è altro che la semplificazione della #27.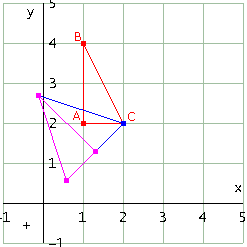

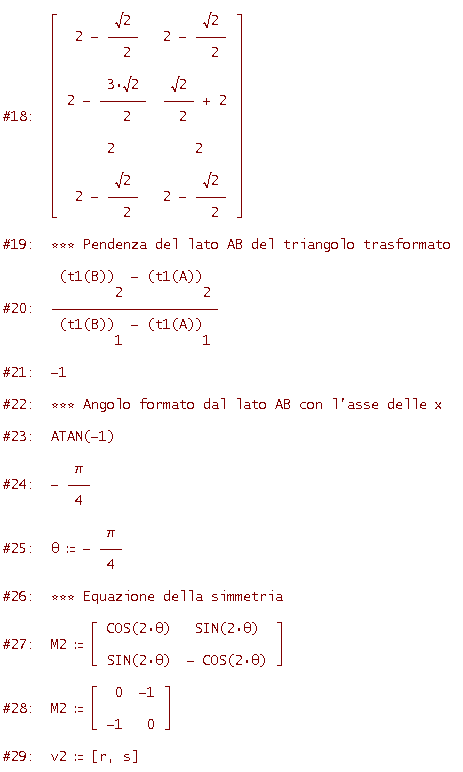
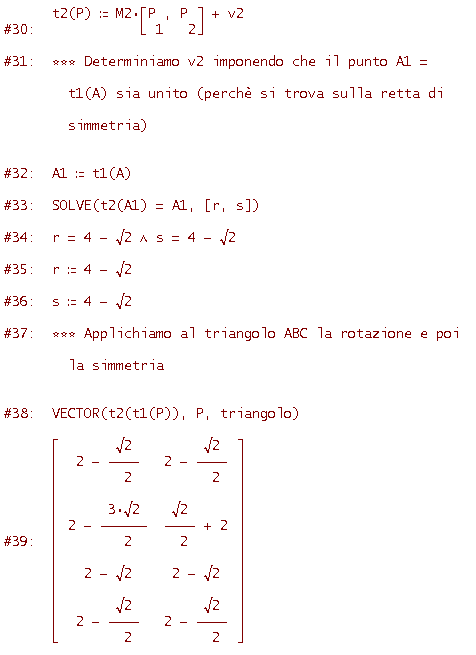
Vediamo qual è la matrice M3 e il vettore v3 della trasformazione composta
Ora qualche semplice osservazione sul (comodo!) calcolo matriciale. Le equazioni in forma matriciale delle due trasformazioni sono
quindi l'equazione della trasformazione composta è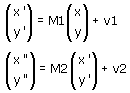
che grazie alle proprietà distributiva e associativa del prodotto di matrici diventa
La matrice della trasformazione composta è quindi M2·M1 e il vettore è M2·v1+v2. Verifichiamolo.