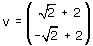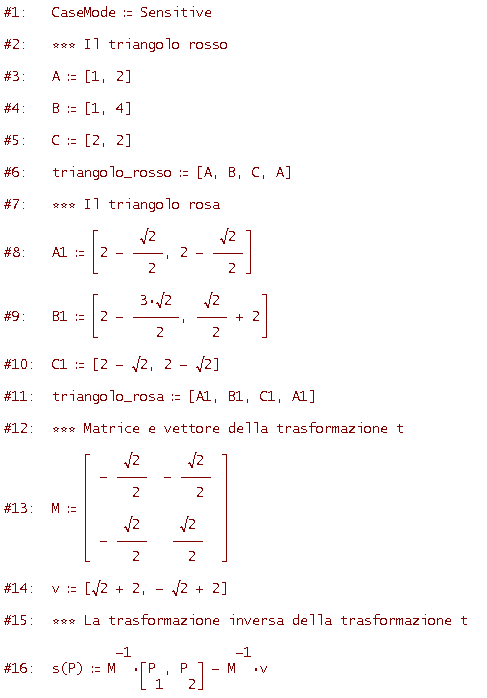Attività successiva
Attività precedente
Indice
Home

Attività 9 - Trasformazioni inverse
In tal modo viene a definirsi una nuova trasformazione del piano, chiamiamola s, che associa al punto P' il punto P. Quindi
La trasformazione s così definita si chiama, come sai, trasformazione inversa di t. Osserva che il prodotto delle trasformazioni s e t (e anche il prodotto di t con s) è uguale alla trasformazione identica, infatti
Te ne rendi conto, semplicemente, ragionando sul diagramma in figura: se applichi a un generico punto P prima t e poi s ritorni a P (quindi ogni punto del piano è unito). E se applichi a un generico punto P' prima s e poi t ritorni a P' (quindi, di nuovo, ogni punto P' del piano è unito). Nota che qui le lettere P' e P, indicando punti generici del piano, hanno lo stesso ruolo, una vale l'altra.
Considera una generica trasformazione lineare t di matrice
(ricorda che det(M) è, per definizione, non nullo). Determina la trasformazione inversa e mostra che si tratta di una trasformazione che è ancora lineare.
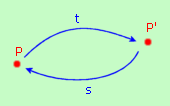 Sia t una trasformazione e P' un punto qualsiasi del piano. Poichè t è una corrispondenza biunivoca, possiamo chiederci quale sia il punto P, l'unico punto P, tale che
Sia t una trasformazione e P' un punto qualsiasi del piano. Poichè t è una corrispondenza biunivoca, possiamo chiederci quale sia il punto P, l'unico punto P, tale che
t(P) = P'
s(P') = P
s(t(P)) = s(P') = P
e anche
t(s(P')) = t(P) = P'

Esperimento 1
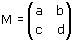

Ecco il codice
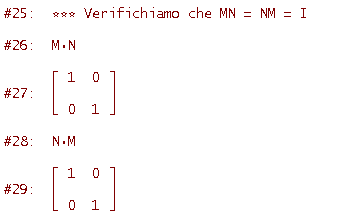
Osserva che il determinante della matrice N è uguale all'inverso del determinante della matrice M (riga #15): poichè M è non nullo anche N sarà non nullo. La matrice N che abbiamo determinato prende il nome di matrice inversa di M ed è tale che
Ciò consegue dal fatto che, come si è visto nell'attività precedente, la matrice del prodotto di due trasformazioni lineari è uguale al prodotto delle matrici delle due trasformazioni e nel nostro caso il prodotto delle trasformazioni è la trasformazione identica (che, come sappiamo, ha per matrice la matrice unità). Facciamo una verifica con Derive
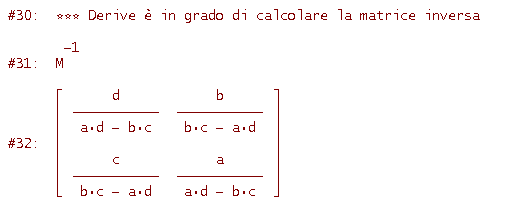
Tieni presente che non tutte le matrici quadrate sono invertibili (o, si dice anche, non singolari): lo sono solo quelle che rappresentano una trasformazione geometrica (corrispondenza biunivoca) cioè quelle che hanno determinante non nullo. La matrice inversa di una matrice M, se esiste, viene indicata col simbolo
M-1Proviamo a far calcolare la matrice inversa di M a Derive
Ora consideriamo una matrice a determinante nullo e verifichiano che non è invertibile
Osservazione 1 Ci siamo resi conto che se t è una trasformazione lineare di matrice M allora la trasformazione inversa di t è la trasformazione lineare di matrice M-1. Inoltre si ha det(M-1) = 1/det(M).
Osservazione 2 E' facile verificare che una trasformazione affine di matrice M e vettore v ha come trasformazione inversa la trasformazione affine di matrice M-1 e vettore -M-1v.

Esperimento 2
Considera l'isometria t, determinata nell'esperimento 2 dell'attività precedente, di matrice
e vettore
che porta il triangolo rosso nel triangolo rosa. Determina la trasformazione inversa e verifica che porta il triangolo rosa nel triangolo rosso.

Ecco il codice
Come vedi, per definire la trasformazione inversa abbiamo tenuto conto dell'osservazione 2.