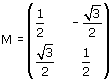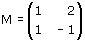Attività successiva
Attività precedente
Indice
Home

Attività 10 - Autovettori e autovalori
Nello studio delle trasformazioni lineari è particolarmente utile sapere quali sono le eventuali rette unite per una trasformazione; una retta r si dice unita se ogni suo punto P è trasformato in un punto P' che appartiene ancora ad r (potendo P' anche coincidere P).
Ora il sistema di equazioni della riga #10, semplificazione della #9,
è un sistema lineare omogeneo in x e y che ammette la soluzione [0, 0]. Tale soluzione, però, non ci interessa perché un autovettore deve essere non nullo; come sai, condizione necessaria e sufficiente affinché un sistema di questo tipo ammetta una soluzione non nulla è che il determinante dei coefficienti sia nullo, cioè sia
Se infatti tale determinante fosse non nullo, per il teorema di Cramer, il sistema ammetterebbe una e una sola soluzione, quindi la soluzione [0, 0]; tieni conto inoltre che tale sistema rappresenta, geometricamente, i punti di intersezione di due rette per l'origine. Tali punti sono la sola origine se il determinante è non nullo (le rette non coincidono) oppure quelli di una retta se il determinante è nullo (le due rette sono coincidenti). L'equazione precedente, nell'incognita k, prende il nome di equazione caratteristica della trasformazione t e, sviluppando il determinante, equivale a
Ti sei reso conto che se k è un autovalore relativo a un certo autovettore [x, y] allora l'equazione precedente deve essere soddisfatta; viceversa si può dimostrare che se k è una soluzione reale dell'equazione allora k è un autovalore per la trasformazione t. Quindi: k è un autovalore per t se e solo se è una radice dell'equazione caratteristica di t.
dove la traccia di M è la somma degli elementi della matrice M che si trovano sulla diagonale principale (dall'alto in basso, da sinistra a destra).
Determina autovettori e autovalori della trasformazione t di matrice
(si tratta di uno stiramento rispetto agli assi coordinati).
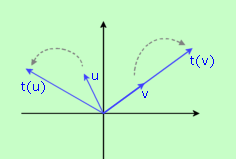 Ecco allora una definizione importante: se t è una trasformazione lineare e v un vettore non nullo, allora v è un autovettore per t se si ha t(v)=kv per un certo numero reale k, cioè se il trasformato di v è un multiplo di v; k prende il nome di autovalore per t. Ad esempio il vettore v in figura è un autovettore mentre non lo è il vettore u. La cosa migliore per cogliere il significato geometrico della nozione di autovettore è utilizzare una figura dinamica di GeoGebra che vale più di qualsiasi definizione.
Ecco allora una definizione importante: se t è una trasformazione lineare e v un vettore non nullo, allora v è un autovettore per t se si ha t(v)=kv per un certo numero reale k, cioè se il trasformato di v è un multiplo di v; k prende il nome di autovalore per t. Ad esempio il vettore v in figura è un autovettore mentre non lo è il vettore u. La cosa migliore per cogliere il significato geometrico della nozione di autovettore è utilizzare una figura dinamica di GeoGebra che vale più di qualsiasi definizione.
E' facile verificare che se v è un autovettore relativo all'autovalore k allora sono autovettori relativi allo stesso autovalore k anche tutti i multipli av di v (dove a, naturalmente, è un numero reale). L'insieme degli autovettori relativi a un autovalore k prende il nome di autospazio di k. L'insieme degli autovalori di t è lo spettro di t.
Vediamo come si fa a determinare gli autovettori e gli autovalori di una trasformazione lineare t. Operiamo con Derive

(a-k)x + by = 0
cx + (d-k)y = 0
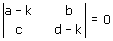
k2 - (a + d)k + (ad - bc) = 0
L'equazione caratteristica della trasformazione lineare t di matrice M può mettersi nella seguente forma, più facile da ricordare,
k2 - traccia(M)·k + det(M) = 0

Esperimento 1
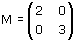

Ecco il codice
Quindi:
tutti i vettori con la punta sull'asse delle x (escluso il vettore nullo, s'intende e non lo diremo più), cioè tutti i vettori del tipo v=[x, 0] con x non nullo, sono autovettori, il relativo autovalore è 2. Ciò significa che l'asse delle x è retta unita cioè ogni suo punto è trasformato in un punto che appartiene ancora all'asse delle x;
tutti i vettori con la punta sull'asse delle y, cioè del tipo [0, y] con y non nullo, sono autovettori, il relativo autovalore è 3. Anche l'asse delle y è retta unita per la trasformazione;
non ci sono altri autovettori.
E' anche facile visualizzare dinamicamente gli autovettori utilizzando le slider bar di Derive. Ecco il codice
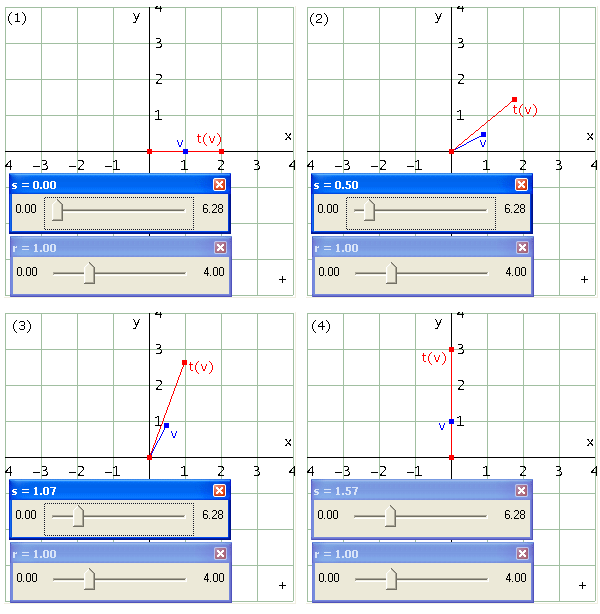
Nota che il generico vettore v non è rappresentato nella solita forma cartesiana [x, y] ma nella più conveniente (per i nostri fini) forma polare [r·cos s, r·sin s]. Inserirai nella finestra grafica una slider bar per il parametro s (con s che varia da 0 a 2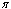 , impostando ad esempio 100 intervalli) e una slider bar per il parametro t (con t che varia, diciamo, da 0 a 4, impostando ad esempio 40 intervalli). Ricordati inoltre di spuntare l'opzione "Aggiorna dinamicamente il grafico". Poi rappresenterai graficamente i segmenti delle righe #21 e #24 rispettivamente in azzurro e in rosso; tali segmenti hanno un vertice nell'origine e rappresentano rispettivamente il vettore v e il suo trasformato. Agendo sulle slider bar puoi studiare il modo in cui si trasforma il vettore v e individuare gli autovettori della trasformazione t. Le figure seguenti mostrano alcune situazioni possibili: nella prima e nella quarta v è un autovettore.
, impostando ad esempio 100 intervalli) e una slider bar per il parametro t (con t che varia, diciamo, da 0 a 4, impostando ad esempio 40 intervalli). Ricordati inoltre di spuntare l'opzione "Aggiorna dinamicamente il grafico". Poi rappresenterai graficamente i segmenti delle righe #21 e #24 rispettivamente in azzurro e in rosso; tali segmenti hanno un vertice nell'origine e rappresentano rispettivamente il vettore v e il suo trasformato. Agendo sulle slider bar puoi studiare il modo in cui si trasforma il vettore v e individuare gli autovettori della trasformazione t. Le figure seguenti mostrano alcune situazioni possibili: nella prima e nella quarta v è un autovettore.

Esperimento 2
Determina autovettori e autovalori della trasformazione t di matrice
(si tratta di una rotazione rispetto all'origine, di 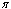 /3 radianti).
/3 radianti).

Ecco il codice
L'equazione caratteristica non ha, come vedi, soluzioni reali, dunque t non ha autovalori e quindi autovettori. Era un risultato prevedibile: una rotazione di 60° cambia la direzione di qualsiasi vettore del piano, non ha rette unite. Verifica ora tu, dinamicamente, che la rotazione t non ha autovettori; utilizzerai delle slider bar come hai già fatto nell'esperimento precedente.

Esperimento 3
Determina le rette unite della trasformazione lineare t dell'esperimento 1 dell'attività 1 di matrice

Ecco il codice
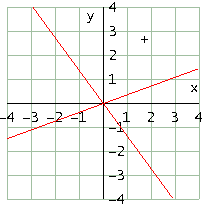
Trovi le equazioni delle due rette unite alle righe #13 e #16 e ne vedi il grafico nella figura seguente.