
 EffeDiX 8.1 - maggio 2025 - Versione freeware gratuita
EffeDiX 8.1 - maggio 2025 - Versione freeware gratuita
Copyright ©2008-2025 Paolo Lazzarini
Sistema: Windows 8/10/11 (32 bit e 64 bit), Windows 7 + .NET Framework 4.8
Requisiti: risoluzione schermo 800x600 o superiore, .NET Framework 4.8 (presente in tutte le più recenti versioni di Windows aggiornate).
Per l'installazione leggi qui.
AI-powered chatbot disponible - Fai clic sull'icona in basso a destra
Sono previsti al max 100 messaggi al mese, sommando le domande di tutti gli utenti e relative risposte dell'agente AI. Quindi il chatbot potrebbe non essere attivo.
N o v i t à d e l l a v e r s i o n e 8.1
N o v i t à d e l l a v e r s i o n e 8.0
Le modifiche del motore grafico riguardano anche molte opzioni già presenti nelle versioni precedenti di EffeDiX; come conseguenza i file .fdx generati con versioni precedenti alla 8.0 non sono compatibili con l'attuale versione. Il problema si risolve tenendo presente che la versione 8.0 può coesistere con le versioni precedenti.
Sarò grato a chiunque voglia segnalarmi eventuali problemi riscontrati nella versione 8.0
O g g e t t i g r a f i c i
 EffeDiX consente di tracciare un'ampia gamma di oggetti grafici:
EffeDiX consente di tracciare un'ampia gamma di oggetti grafici:
- grafici di funzioni
- grafici di successioni
- grafici di funzioni definite a tratti
- luoghi di punti
- grafico della derivata prima e seconda
- grafici di successioni di somme parziali
- curve parametriche
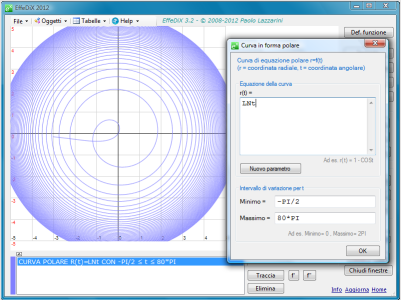
- curve polari
- curve spline
- grafici a dispersione
- curve di regressione (lineare, quadratica, cubica, funzione potenza, esponenziale, logaritmica)
- campi vettoriali
- campi di direzione
- curve integrali (primitive, soluzioni di equazioni differenziali del primo ordine, del secondo ordine, di sistemi autonomi o non autonomi di due equazioni differenziali)
- plurirettangoli (relativi a somme di Riemann)
- orbite discrete 1D (diagrammi a ragnatela)
- orbite discrete 2D
- diagramma delle orbite al variare di un parametro (diagramma di biforcazione)
- diagramma delle orbite al variare del punto iniziale
- bacino di attrazione mappa 2D
- filled Julia set mappa 2D
- escaping set mappa 2D
- domini normali
- domini descritti in coordinate polari
- tracciamento e animazione di vettori tangenti e normali a una curva parametrica
- tracciamento di campi vettoriali su una curva parametrica
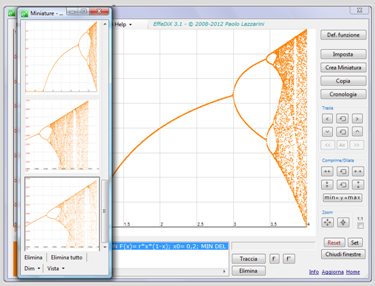 Sono inoltre presenti svariate opzioni per tracciare: punti, intorni, segmenti, vettori, rette, poligoni, circonferenze, ellissi, parabole, iperboli, semipiani.
Sono inoltre presenti svariate opzioni per tracciare: punti, intorni, segmenti, vettori, rette, poligoni, circonferenze, ellissi, parabole, iperboli, semipiani.
La qualità degli oggetti grafici è notevole essendo supportato l'antialiasing e il rendering 3D per tutti gli oggetti grafici.
Il programma è stato progettato per essere utilizzato nel modo più semplice ed intuitivo e fornisce tutti gli strumenti di base per studiare un qualsiasi oggetto grafico; potrete operare traslazioni, compressioni, dilatazioni, zoomate utilizzando il mouse o facendo clic su dei pulsanti. Potrete inoltre generare facilmente e rapidamente svariati tipi di tabelle.
Una caratteristica del programma, che lo distingue da ambienti simili, consiste nella possibilità di animare lo scorrimento continuo del grafico di una funzione (o di una successione) verso destra o verso sinistra; in ogni frame dell'animazione il grafico viene tracciato, se possibile, tra il suo minimo e il suo massimo: in tal modo potrete osservare in modo continuo la sua evoluzione.
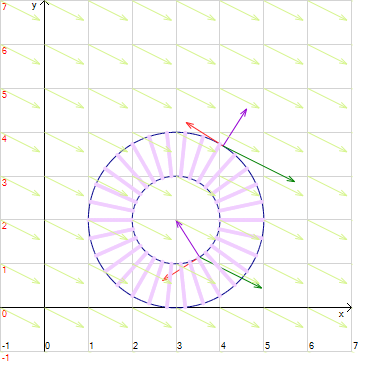
 EffeDiX vi consente inoltre di studiare delle famiglie parametriche di funzioni utilizzando per ciascun parametro una slider bar; potrete anche animare un grafico facendo variare con continuità un parametro.
EffeDiX vi consente inoltre di studiare delle famiglie parametriche di funzioni utilizzando per ciascun parametro una slider bar; potrete anche animare un grafico facendo variare con continuità un parametro.
Tutti gli oggetti grafici di EffeDiX possono essere definiti utilizzando parametri; ad esempio potrete inserire il punto di coordinate (COSt, SINt) avendo dichiarato il parametro t che varia nell'intervallo [0, 2PI]. EffeDiX creerà una slider bar che vi consentirà di pilotare il punto facendo variare t oppure di animare il moto del punto facendo variare in modo automatico il parametro t.
C a l c o l o n u m e r i c o
Tutti gli algoritmi di calcolo utilizzati da EffeDiX sono algoritmi numerici, non simbolici. Tutte le soluzioni sono numeriche. Le opzioni disponibili:
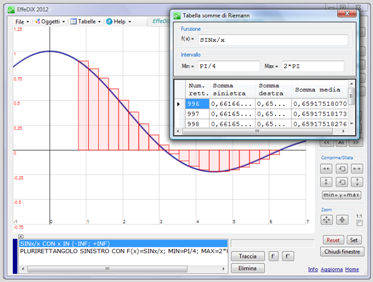
- soluzione di equazioni e di sistemi di equazioni
- ricerca di massimi e minimi
- generazione di tabelle numeriche per funzioni reali di variabile reale
- generazione di tabelle numeriche per derivate prime e seconde
- generazione di tabelle numeriche per somme parziali
- generazione di tabelle numeriche per somme di Riemann
- generazione di tabelle numeriche per curve parametriche
- generazione di tabelle numeriche per orbite discrete 1D e 2D
- integrali indefiniti (primitive)
- equazioni differenziali del primo e secondo ordine
- sistemi di due equazioni differenziali (autonomi o non autonomi)
- generazione di tabelle numeriche per le soluzioni di equazioni e sistemi di equazioni differenziali
- bacino di attrazione di un punto di equilibrio per un sistema autonomo di equazioni differenziali
- integrali definiti
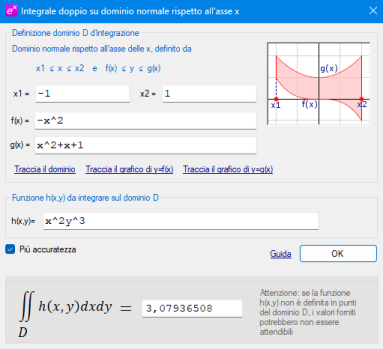
- integrali doppi su domini normali
- integrali doppi su domini descritti in coordinate polari
- integrali doppi su settori di dominio ellittico
- integrali curvilinei di prima specie
- integrali di forme differenziali
- integrali di flusso
- integrali complessi
- autovalori, autovettori, autospazi matrice 2x2
- matrice jacobiana
I n s t a l l a z i o n e d e l l a v e r s i o n e 8.1
 Win 7/8/8.1/10/11
Win 7/8/8.1/10/11
Se il sistema operativo è Windows 11/10/8/8.1/7 non dovete far altro che scaricare il file EffeDiX_8.1_setup.zip e lanciare l'installer EffeDiX_8.1_setup.exe. Saranno anche installati il file FAQ.pdf ("Domande frequenti") e la Guida. Se connessi avrete accesso alla videoguida.
Se Microsoft Defender dovesse impedire l'installazione ("Autore non riconosciuto"), fare clic su "Ulteriori informazioni" e poi su "Esegui comunque". Il file eseguibile EffeDiX.exe dispone di firma digitale.
Se il sistema operativo è Windows 7 potrebbe essere necessario installare la versione 4.8 del Framework .NET (scaricabile gratuitamente dal sito di Microsoft), comunque l'installer verificherà se sia necessario questo aggiornamento.
E s e m p i (senza commento audio)
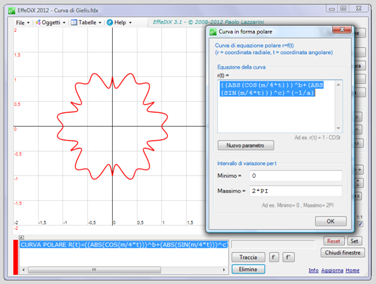
0 ≤ t ≤ 2π, al variare con continuità di n
U s a r e E f f e Di X i n p o c h i m i n u t i
Qui di seguito trovate una serie di video che mostrano concretamente, almeno negli aspetti essenziali, come utilizzare il programma.
![]() Primi passi (1)
Primi passi (1)
Sistema di riferimento monometrico o dimetrico. Menu oggetti. Come inserire l'espressione analitica di una funzione. Come impostare il dominio di una funzione. Box degli oggetti grafici. Tracciare il grafico di una funzione. Come modificare la regione di piano visualizzata mediante pulsanti: zoomare, comprimere, dilatare. Pulsanti RESET e SET. Trascinare il piano. Zoom locale. Colore degli oggetti. Eliminare oggetti. Finestra delle impostazioni: come modificare la regione di piano visualizzata. Impostare la griglia sul piano. Come introdurre simboli nei campi di EffeDiX.
![]() Primi passi (2)
Primi passi (2)
Cronologia. Campo delle coordinate del cursore. Tabella x, f(x). Significato dei colori nella tabella x, f(x). Tracciare un punto dalla tabella. Interattività delle finestre di servizio di EffeDiX. Come modificare la griglia sul piano cartesiano.
![]() Studio del grafico di una funzione
Studio del grafico di una funzione
Massimo e minimo assoluto di una funzione in un intervallo dato. Punti di massimo e minimo relativo. Grafico della derivata della funzione selezionata. Visualizzare nel piano l'etichetta e le coordinate di un punto. Grafico della derivata seconda. Concavità di una funzione. Punti di flesso. Tangente in un punto di flesso. Versore tangente. Pulsanti di scorrimento (<<, >>).
![]() Ancora studio del grafico di una funzione
Ancora studio del grafico di una funzione
Salvare gli oggetti grafici e le impostazioni. Aprire la finestra di impostazione di un oggetto già inserito (per modificarlo). Help sui pulsanti nella definizione di una funzione. Asintoti obliqui di una funzione. Valutare limiti di una funzione. Scorrimento lungo gli asintoti. Informazioni sul dominio naturale di una funzione. Non derivabilità e tangente verticale.
![]() Grafico di una funzione dipendente da un parametro
Grafico di una funzione dipendente da un parametro
Come utilizzare parametri. Slider bar di controllo di un parametro. Spessore di un oggetto. Animazioni. Opzioni presenti sulla slider bar di un parametro. Come modificare l'escursione di un parametro. Uso dei tasti freccia della tastiera per muovere il cursore di una slider bar. Come determinare gli zeri di una funzione: punto di intersezione di due grafici. Tracciare un punto dinamico. Tangente dinamica al grafico di una funzione.
![]() Grafico di una funzione definita a tratti
Grafico di una funzione definita a tratti
Come definire una funzione a tratti. Continuità e derivabilità di una funzione definita a tratti. Non esistenza della tangente in un punto angoloso.
![]() Risolvere un'equazione o un sistema
Risolvere un'equazione o un sistema
Risolvere un'equazione posta nella forma f(x)=0. Utilizzare una tabella per verificare se un'equazione in un'incognita ammette soluzioni intere. Determinare il punto di intersezione di due grafici. Lavorare con finestre affiancate. Risolvere un sistema di due equazioni in due incognite posto nella forma y=f(x) ∧ y=g(x). Tracciare una circonferenza ed ottenerne l'equazione. Punti di intersezione di una circonferenza e di un grafico di funzione.
![]() Discutere un'equazione parametrica
Discutere un'equazione parametrica
Discussione dell'equazione parametrica di secondo grado kx2+x+k=0. Grafico dinamico della parabola y=kx2+x+k. Rappresentazione dinamica degli zeri del trinomio, di k e del delta del trinomio. Grafico del delta in funzione di k. Inversione di concavità della parabola al variare di k. Significato grafico dell'abbassamento di grado dell'equazione per k=0.
![]() Tracciare una curva parametrica. Moto di un punto. Vettori.
Tracciare una curva parametrica. Moto di un punto. Vettori.
Equazioni parametriche di una famiglia di ellissi. Moto piano su traiettoria ellittica. Vettori velocità e accelerazione. Proiezione di un vettore. Componenti tangenziale e centripeta del vettore accelerazione. Circonferenza per tre punti. Circonferenza osculatrice. Curvatura e centro di curvatura. Moto circolare uniforme.
![]() Grafico di una primitiva di una funzione f(x)
Grafico di una primitiva di una funzione f(x)
Come tracciare il grafico della primitiva F(x) della funzione f(x) tale che F(x0)=y0. Come impostare l'intervallo, contenente x0, in cui la primitiva sarà tracciata. Come impostare l'accuratezza della soluzione. Come utilizzare la tabella numerica.
![]() Equazioni differenziali del primo ordine
Equazioni differenziali del primo ordine
Grafico della soluzione y(x) dell'equazione differenziale y'=f(x, y) con la condizione iniziale y(x0)=y0 (problema di Cauchy). Come impostare l'intervallo, contenente x0, in cui sarà tracciata la soluzione. Come impostare l'accuratezza della soluzione. Come utilizzare la tabella numerica. Animare le soluzioni al variare della condizione iniziale.
![]() Equazioni differenziali del secondo ordine
Equazioni differenziali del secondo ordine
Grafico della soluzione y(x) dell'equazione differenziale y'' = f(x, y, y') con le condizioni iniziali y(x0)=a, y'(x0)=b (problema di Cauchy). Come impostare l'intervallo, contenente x0, in cui sarà tracciata la soluzione. Come impostare l'accuratezza della soluzione. Rappresentare graficamente le condizioni iniziali. Animare le soluzioni al variare delle condizioni iniziali. Equazione differenziale di un pendolo caotico. Dipendenza critica dalle condizioni iniziali.
![]() Sistemi autonomi di equazioni differenziali
Sistemi autonomi di equazioni differenziali
Grafico della soluzione (x(t), y(t)) del sistema autonomo di equazioni differenziali x'=f(x, y), y'=g(x, y) con le condizioni iniziali x(0)=a, y(0)=b (problema di Cauchy). Come impostare l'intervallo del tempo t, contenente t=0, in cui sarà tracciata la soluzione. Tracciare il campo di direzioni relativo al sistema. Tabella numerica relativa alla soluzione del sistema. Come visualizzare in un punto della traiettoria il valore del tempo t. Come tracciare il campo dei vettori velocità, interpretando la curva soluzione come la traiettoria di una particella in movimento.
![]() Ancora sistemi autonomi di equazioni differenziali
Ancora sistemi autonomi di equazioni differenziali
Punti critici di un campo vettoriale. Soluzioni di equilibrio. Stabilità di una soluzione di equilibrio. Ritratto di fase per un sistema non lineare. Punti critici attrattori e repulsori.
![]() Sistemi di equazioni differenziali (autonomi o non autonomi)
Sistemi di equazioni differenziali (autonomi o non autonomi)
Differenza tra sistemi autonomi e non autonomi. Impostazioni per un sistema non autonomo. Come tracciare il vettore velocità relativo a un punto della traiettoria in un dato istante.
G u i d a a d a l c u n e o p z i o n i
 Grafico di una successione di somme parziali
Grafico di una successione di somme parziali
 Somme di Riemann
Somme di Riemann
 Primitive di una funzione
Primitive di una funzione
 Equazioni differenziali del primo ordine
Equazioni differenziali del primo ordine
 Equazioni differenziali del secondo ordine
Equazioni differenziali del secondo ordine
 Sistemi autonomi di equazioni differenziali
Sistemi autonomi di equazioni differenziali
 Sistemi di equazioni differenziali (autonomi o non autonomi)
Sistemi di equazioni differenziali (autonomi o non autonomi)
 Bacino di attrazione di un punto di equilibrio per un sistema autonomo di equazioni differenziali
Bacino di attrazione di un punto di equilibrio per un sistema autonomo di equazioni differenziali
 Campi vettoriali
Campi vettoriali
 Sistemi dinamici discreti: orbite 1D
Sistemi dinamici discreti: orbite 1D
 Sistemi dinamici discreti: orbite 2D
Sistemi dinamici discreti: orbite 2D
 Diagramma delle orbite al variare di un parametro r (diagramma di biforcazione)
Diagramma delle orbite al variare di un parametro r (diagramma di biforcazione)
 Diagramma delle orbite al variare del punto iniziale x0
Diagramma delle orbite al variare del punto iniziale x0
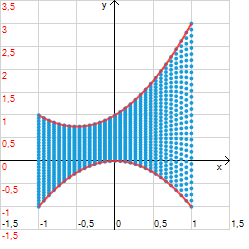
 Integrali doppi su domini normali
Integrali doppi su domini normali
 Integrali doppi su domini descritti in coordinate polari
Integrali doppi su domini descritti in coordinate polari
 Integrali doppi su domini ellittici o settori di dominio ellittico
Integrali doppi su domini ellittici o settori di dominio ellittico
 Integrali curvilinei di prima specie
Integrali curvilinei di prima specie
 Integrali di forme differenziali (curvilinei di seconda specie)
Integrali di forme differenziali (curvilinei di seconda specie)
 Integrali di flusso
Integrali di flusso
 Integrali complessi
Integrali complessi
 Funzioni integrali
Funzioni integrali
 Sistemi dinamici discreti di dimensione uno
Sistemi dinamici discreti di dimensione uno
 Autovalori, autovettori, autospazi
Autovalori, autovettori, autospazi
 Matrice jacobiana
Matrice jacobiana
 Bacino di attrazione mappa 2D
Bacino di attrazione mappa 2D
 Filled Julia set ed escaping set mappa 2D
Filled Julia set ed escaping set mappa 2D
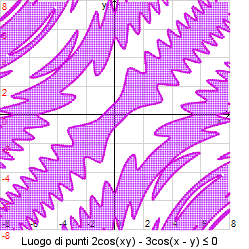
 Luogo di punti
Luogo di punti
 Soluzioni di un aistema di equazioni
Soluzioni di un aistema di equazioni
 Equazioni differenziali del secondo ordine: problemi con condizioni al bordo
Equazioni differenziali del secondo ordine: problemi con condizioni al bordo
Tutti i file della guida sono già presenti nel pacchetto di installazione di EffeDiX.
D o m a n d e f r e q u e n t i
Domande frequenti  FAQ
FAQ
Il file FAQ.pdf è già presente nel pacchetto di installazione di EffeDiX.
